Dot products and duality

What to learn

  • Principle of dot product

    Description

  • Why is \(\vec{v} \cdot \vec{w} = \vec{w} \cdot \vec{v}\) true?

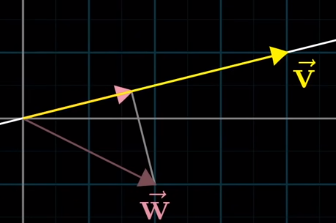
    • Let’s think same length vectors \(\vec{v},\vec{w}\) linear_algebra_1.PNG

      we can draw line that makes equal angle between them. And projecting each other makes same length of projected line!

    • Let’s think other length vectors $2\vec{v},\vec{w}$

      linear_algebra_2.PNG the length of \(\vec{v}\) has doubled.

      \((2\vec{v})\cdot\vec{w} = 2 \vec{v}\cdot\vec{w}\)!

      linear_algebra_3.PNG

      the length of projected \(\vec{v}\) has doubled.

      \((2\vec{v})\cdot\vec{w} = 2 \vec{v}\cdot\vec{w}\)! (It is defined even in situations where the length is not the same.)

    • So, we know \(\vec{v} \cdot \vec{w} = \vec{w} \cdot \vec{v}\)!

  • Why calculate dot product numerically has relation with projection?

    • \(\vec{a} = \begin{bmatrix}a & b\end{bmatrix}\) means projecting two columns to one dimension. and if we want to make projected vector \(\vec{x} = \begin{bmatrix}x & y\end{bmatrix}^T\)by \(\vec{a}\), think like this. projected vector is obtained by same scaling with projected basis.

      \[\vec{i} = \begin{bmatrix}1 \\ 0\end{bmatrix} \rightarrow a, \vec{j} = \begin{bmatrix}0 \\ 1\end{bmatrix} \rightarrow b,\]

      So, \(\vec{a}\cdot\vec{x}^T = ax+by\)

    • One line projection to another line is linear transformation.

      • Let’s defined direction vector \(\vec{u}\) of any line. Then we can easily find projection matrix\(A = \begin{bmatrix}a & b\end{bmatrix}\) using drawing symmetry line technic! → \(A = \begin{bmatrix}u_x & u_y\end{bmatrix}\). and computing this transformation for arbitrary vector in that space requires multiplying that matrix by those vector \(\vec{x}^T = \begin{bmatrix}x \\ y\end{bmatrix}\)

        \[\begin{bmatrix}u_x & u_y\end{bmatrix} \begin{bmatrix}x \\ y\end{bmatrix} = u_x \cdot x + u_y \cdot y\]
      • Similar way, using vector \(\vec{v} = 3\vec{u} = \begin{bmatrix}3u_x & 3u_y\end{bmatrix}\)(length becomes >1).then new transformation matrix will be defined new matrix \(A = \begin{bmatrix}3u_x & 3u_y\end{bmatrix}\) and equally calculated.
      • So we know Why calculate dot product numerically has relation with projection.
    • duality
      • 1x2 matrices ↔ 2d vectors!

        Next Step

  • Cross products

    References

  • https://www.youtube.com/watch?v=LyGKycYT2v0&list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab&index=9