Convolutional Layer

  1. Background
    • MLP
  2. Description
    • CNN의 기본 가정은 stationarity of statistics, locality of pixel dependencies
      • stationarity of statistics : 어떤 데이터 내의 통계적 특성은 시간 혹은 위치에 상관없이 동일 패턴이 반복된다는 의미 → 이미지내에서 같은 물체는 같은 패턴의 rgb분포를 이루고 있을 확률이 높다. → convolution연산을 한 featuremap은 equivariance한 특성을 가짐.
      • locality of pixel dependencies : 이미지 내에서 한 픽셀은 주변의 인접한 픽셀들과 correlation이 높다.(멀리 떨어진 픽셀보다 가까이 있는 픽셀과 연관되어있을확률이 높다.) → kernel은 input data의 일부분씩 확인(한다고 표현할 수 있다.)
    • convolution 연산을 한 featuremap은 특정 edge에 반응하거나, blob등 지역적 특성에 반응하여 input data의 feature를 extraction할 수 있는 도구라고 생각할 수 있다. → feature detection.
      • input data에 가까운 convolution layer일수록, 간단한 특성들에 반응한다. layer가 깊어질수록, 이런 특성들을 모아 추상적인 정보를 전달할 수 있게 된다.
    • 1d convolution 설명
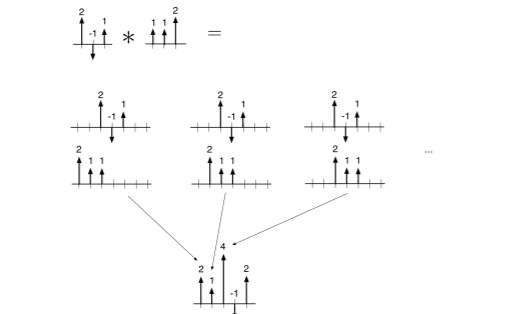
      • \((x * w)[t] = \sum_\tau x[t-\tau]w[\tau]\)로, \(x\)를 flip한 뒤, t 만큼 평행이동한 것과 같다. 밑에서 설명하겠지만 교환법칙이 성립하니 아래와 같은 예시로 설명을 들자면,

      cnn_1.PNG

      • \(\begin{bmatrix} 2\\ -1\\ 1 \end{bmatrix}*\begin{bmatrix} 1\\ 1\\ 2 \end{bmatrix}\)는 다음과 같이 좌우로 padding을 2씩 주어(t를 기준값보다 -2~+2까지 구해보면) 다음과 같이 계산 가능하다.

        \[\begin{bmatrix}2 \times 0+1 \times 0 + 1 \times 2 \\ 2 \times 0+1 \times 2 + 1 \times -1 \\ 2 \times 2+1 \times -1 + 1 \times 1 \\ 2 \times -1+1 \times 1 + 1 \times 0 \\ 2 \times 1+1 \times 0 + 1 \times 0 \end{bmatrix} = \begin{bmatrix} 2\\ 1 \\ 4 \\ -1 \\ 2\end{bmatrix}\]

      • 이를 행렬로 연산하면,

        \[\begin{bmatrix} 2\\ -1\\ 1 \end{bmatrix}*\begin{bmatrix} 1\\ 1\\ 2 \end{bmatrix} = \begin{bmatrix} 1&0&0\\ 1&1&0\\ 2&1&1\\0&2&1\\0&0&2 \end{bmatrix}\begin{bmatrix} 2\\ -1\\ 1 \end{bmatrix} = \begin{bmatrix} 2\\ 1\\ 4\\-1\\2 \end{bmatrix}\]

        다음과 같이 나타낼 수 있다.

    • 2d convolution 설명

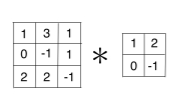
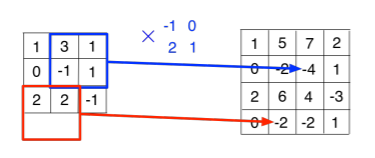
      • 1d convolution에서 확장하면, \((x * w)[s,t] = \sum_{\sigma,\tau} x[s- \sigma,t-\tau]w[\sigma,\tau]\)로 나타낼 수 있다.

        cnn_2.PNG

      cnn_3.PNG

      \[\begin{bmatrix} x_{11}&x_{12}&x_{13}\\ x_{21}&x_{22}&x_{23}\\ x_{31}&x_{32}&x_{33}\\ \end{bmatrix}*\begin{bmatrix} k_{11}&k_{12} \\ k_{21}&k_{22}\end{bmatrix} = \begin{bmatrix} k_{22}&0&0&0&0&0&0&0&0&0&0&0&0&0&0&0\\k_{21}&k_{22}&0&0&0&0&0&0&0&0&0&0&0&0&0&0\\0&k_{21}&k_{22}&0&0&0&0&0&0&0&0&0&0&0&0&0\\0&0&0&k_{21}&0&0&0&0&0&0&0&0&0&0&0&0\\k_{12}&0&0&k_{22}&0&0&0&0&0&0&0&0&0&0&0&0\\k_{11}&k_{12}&0&k_{21}&k_{22}&0&0&0&0&0&0&0&0&0&0&0\\0&k_{11}&k_{12}&0&k_{21}&k_{22}&0&0&0&0&0&0&0&0&0&0\\0&0&k_{11}&0&0&k_{21}&0&0&0&0&0&0&0&0&0&0\end{bmatrix}\begin{bmatrix}x_{11}\\x_{12}\\x_{13}\\x_{21}\\x_{22}\\ x_{23}\\ x_{31}\\x_{32}\end{bmatrix}\]

      위의 방식으로 진행되게 됨. 이후 계산 생략.

    • properties
      • 교환 법칙, 분배 법칙, 결합 법칙이 모두 성립함.
      • \[u*v = v * w\]
      • \[(u*v)*w = u*(v*w)\]
      • \[(ax+b')*w = ax*w + bx'*w\]
      • \[x*(aw+bw') = ax*w+bx*w'\]
    • 왜 Auto diff library에서는 cross-correlation을 쓰는지?
      • 구현상 flip에 추가연산을 써야해 연산은 사실 cross-correlation이지만 차이점은 filter가 그냥 flip된 representation을배우는것뿐임. 하지만 행렬 연산으로 봤을 때는 큰 차이가 없다. 1 dimension convolution을 보면 다음과 같다. 참고로, cross-correlation은 교환법칙이 성립하지 않음.
      \[\begin{bmatrix} 2\\ -1\\ 1 \end{bmatrix}\star\begin{bmatrix} 1\\ 1\\ 2 \end{bmatrix} = \begin{bmatrix} 1&0&0\\ 1&2&0\\ 1&1&2\\0&1&1\\0&0&1 \end{bmatrix}\begin{bmatrix}2\\-1\\1 \end{bmatrix} = \begin{bmatrix}2\\0\\3\\0\\1 \end{bmatrix}\]
    • featuremap size
      • \[OutputWidth = \frac{Input Width+2Padding-KernelWidth}{Stride}+1\]
      • \[OutputHeight = \frac{Input Height+2Padding-KernelHeight}{Stride}+1\]
    • parameter 수
      • (Kernel size) * (Input channel) * (Output channel) + (Output Channel)
        • (Kernel width) * (Kernel height) * (Input channel) * (Output channel) + (Output Channel)
    • Backprop

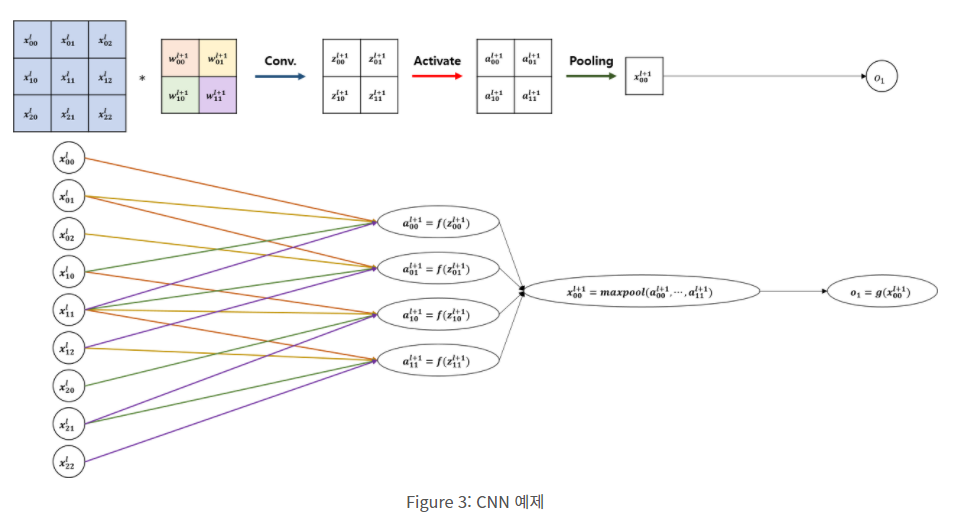
      • 일반 MLP에서, local connection이 되었고, kernel weights만 share한다는 점을 유의하면 쉽게 backpropagation할 수 있다. 참고를 돕기 위한 그림과 더 설명이 필요하면 reference를 따라가면 된다.

        cnn_4.PNG

    • Pooling
      • invariance를 얻기위해 사용된다. invariance를 왜 얻어야 하고 얻음으로써의 단점은 무엇일까?
        • convolution 연산은 위에서 봤다시피 equivariant한 연산이다. 이는 정보의 변화에 따른 결과값도 변화가 있다는 뜻이다. 하지만 classification등의 task에서는 이러한 특성이 generalization을 어렵게 한다. 그렇기 때문에, 비가역적이기 때문에 정보의 손실이 있음에도 maxpooling을 통해 invariance함을 얻어가기 위해 자주쓰이고 있다. 극단적인 예로 채널 내의 최대값만을 maxpooling해가는 경우도 있다. 하지만 image segmentation, object detection 분야에서는 equivariant하기 위해 + 정보의 손실을 막기 위해 여러가지 기법을 사용한다.
      • receptive field 키우기위함
        • data의 object 크기가 dynamic해도, kernel의 크기는 고정되어 있기 때문에, parameter개수를 늘리지않으면서 receptive field를 넓히는 간단한 방법중 하나는 pooling이다.
    • 문제점
      • kernel을 사용함으로써, 한 커널이 물체의 회전 및 크기 변환에 대해 모두 알 수 없기 때문에, 데이터를 augmentation하는 방식으로 현재 해결중+capsule net
      • 한 물체라고 해도, 각각의 객체에 대한 위치를 encoding하지않기때문에, 하나의 물체를 이루는 여러요소들의 위치에 대한 고려가 이루어지지 않음. capsule net으로 해결하려함
  3. Next Step
    • RNN도 정리해볼 예정..
  4. References