1. Background
    • ..
  2. Description
    • Long Short-Term Memory Recurrent Neural Network Architectures for Large Scale Acoustic Modeling(2014)에서 나오는 RNN의 특징을 살펴보면 다음과 같다.
      • Recurrent neural networks contain cycles that feed the network activations from a previous time step as inputs to the network to influence predictions at the current time step. These activations are stored in the internal states of the network which can in principle hold long-term temporal contextual information.

        • 이는 기존 Directed Acyclic Graph구조와는 다르게, 이전의 network activation이 현재 시점의 영향을 주는 cycle을 가지고 있다는 것이다. 이는 내부에 long term temporal contextual information을 잘 encoding한 state를 들고있다는 것인데, 이를 통해 해결할 수 있는 문제들을 보겠다. 일반적인 Multi Layer Perceptron 구조라면, sequential한 task에서 memoryless라는 단점이 있다. 이전의 결과에 영향을 받아 결과를 내야하는 task에서 시점 T에서의 결과의 확률을 수식으로 나타내면 다음과 같다.

          \[p(w_1,...,w_T) = \prod_{t=1}^T {p(w_t |w_1,...,w_{t-1}})\]

          이때, 일반적인 Multi Layer Perceptron으로 설계하게 된다면, 아래 그림과 같이 설계할 수 있다. 이는 결과가 바로 이전의 상태에서만 영향을 받는 Markov한 상황이 된다.

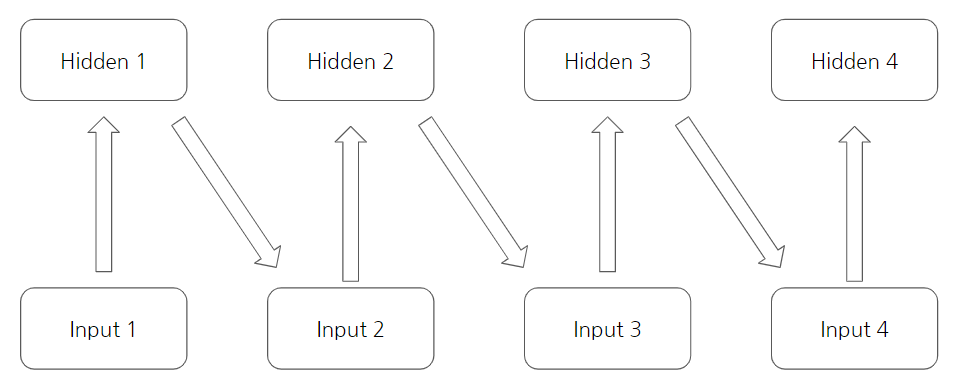
          rnn_1.PNG

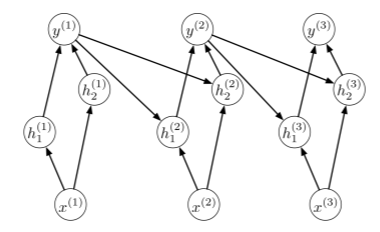
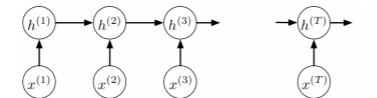
          \[p(w_t|w_1,...w_{t-1}) = p(w_t|w_{t-1})\]

          이는 결과에 영향을 주는 이전의 context를 적절히 embedding할 수 없다는 것을 의미하고, 이를 단순히 사고실험으로, 위에서 찾아본 RNN의 특징을 생각하면 아래 그림과 같이 hidden끼리의 connection을 주면 Hidden state 해결할 수 있다는 것을 도출할 수 있다.

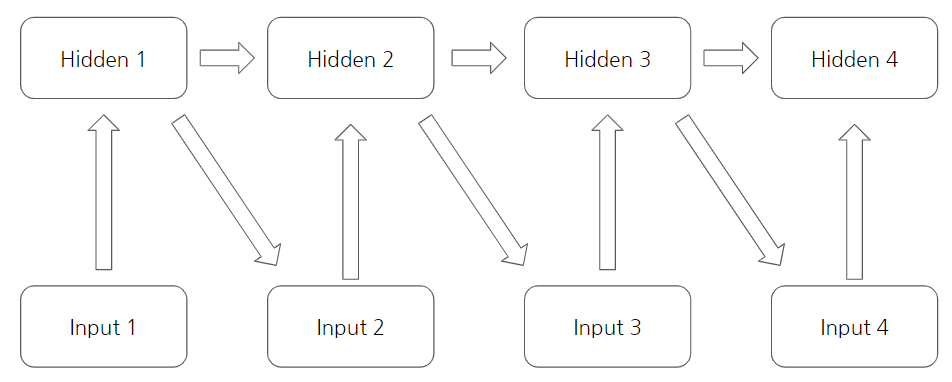
          rnn_2.PNG

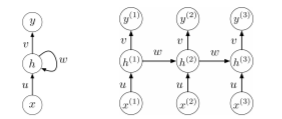
        이는 설명하기 쉽게 하기 위해 위처럼 unrolled상태로 나타냈지만, 실제 Recurrent Network는 아래 그림의 좌측과 같다. 간단한 recurrent computation에 대한 예제 세가지를 보자면 다음과 같다.

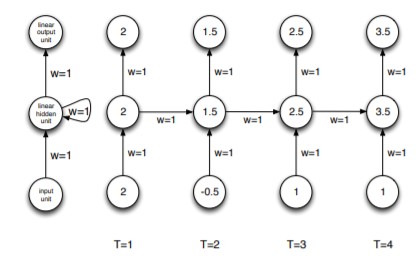
        • example 1

          rnn_3.PNG

          \[x_1 = 2,h_1 = w_{x}x_1+w_hh_0 = 1+0 \cdot2, y_1 = w_{y}h_1 = 1 \cdot 2\] \[x_2 = -0.5,h_2 = w_{x}x_2 + w_{h}h_1 = 1\cdot -0.5+1 \cdot2, y_2 = w_{y}h_2 = 1 \cdot 1.5\] \[x_3 = 1,h_3 = w_{x}x_3 + w_{h}h_2 = 1\cdot 1+1 \cdot1.5, y_3 = w_{y}h_2 = 1 \cdot 2.5\] \[x_4 = 1,h_4 = w_{x}x_4 + w_{h}h_3 = 1\cdot 1+1 \cdot2.5, y_4 = w_{y}h_3 = 1 \cdot 3.5\]

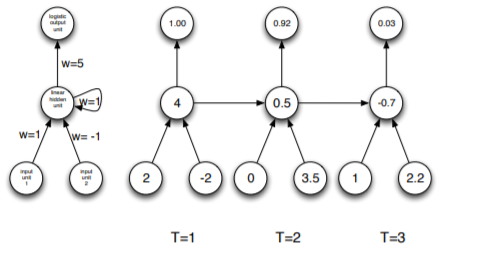
        • example 2

          rnn_4.PNG

          \[x_{11} = 2,x_{12} = -2,h_1 = w_{x_{1}}x_{11}+w_{x_{2}}x_{12}+w_hh_0 = 1\cdot2+-1\cdot-2+1\cdot0, y_1 = \frac{1}{1+e^{-w_{y}h_1}} = \frac{1}{1+e^{5 \cdot 4}}\] \[x_{21} = 0,x_{22} = 3.5,h_1 = w_{x_{1}}x_{11}+w_{x_{2}}x_{12}+w_hh_0 = 1\cdot0+-1\cdot3.5+1\cdot4, y_1 = \frac{1}{1+e^{-w_{y}h_1}} = \frac{1}{1+e^{5 \cdot 0.5}}\] \[x_{31} = 1,x_{32} = 2.2,h_1 = w_{x_{1}}x_{11}+w_{x_{2}}x_{12}+w_hh_0 = 1\cdot1+-1\cdot2.2+1\cdot0.5, y_1 = \frac{1}{1+e^{-w_{y}h_1}} = \frac{1}{1+e^{5 \cdot -0.7}}\]

        • example 3

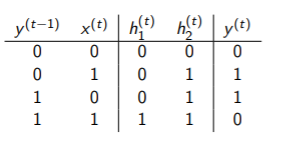
          • 마지막은 parity bit에 대한 예제인데, 지금까지 데이터내의 1이 홀수일 경우,1 짝수일경우 0 이 나오는 문제이다. 이는 다음과 같다.

            \[\begin{matrix} Input : 0,1,0,1,1,0,1,0,1,1 \\ Parity bits : 0,1,1,0,1,1,0,0,1,0 \end{matrix}\]

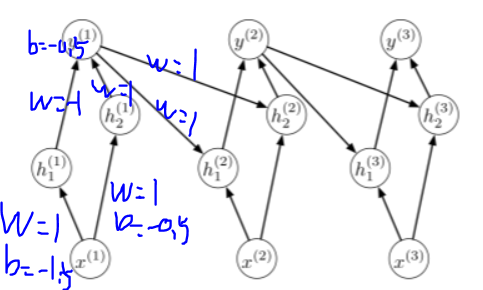
          • XOR문제이므로, 이를 간단히 해결하기 위해선 다음과 같이 hidden layer가 필요하다.

            rnn_5.PNG

            그리고, 이를 해결하기 위해, hidden state에서 xor를 해결하도록 한 케이스에 대한 표를 만들면 다음과 같다.

            rnn_6.PNG

            그리고 이처럼 값을 만들기 위해 weights와 activation function을 조정하면, 다음과 같다.

            rnn_7.PNG

            activation function은 0보다 클경우 1, 0과 같거나 작을 때 0 이면, 문제를 해결할 수 있음을 알 수 있다.

    • backpropagation

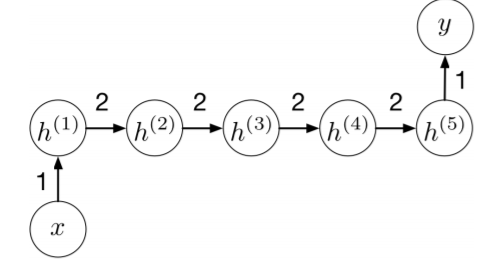
      • 위의 example에서 했던것 처럼 그림의 우측과 같이 unrolled해야 계산하기 쉽기 때문에, 우측을 통해 \(z^{(t)},h^{(t)}, y^{(t)}\)를 나타내 보겠다.

        rnn_8.PNG

        \[\begin{matrix} z^{(t)} = ux^{(t)}+wh^{(t-1)}\\ h^{(t)} = \phi(z^{(t)})\\ r^{(t)} = vh^{(t)}\\ y^{(t)} = \phi(r^{(t)}) \end{matrix}\]

        \(\phi\)로는 보통 tanh를 사용하며, result에서 오는 loss signal \(L\)과의 편미분을 통해 \(\frac{\partial L}{\partial v},\frac{\partial L}{\partial w},\frac{\partial L}{\partial u}\)를 구하면 된다.

        \[\frac{\partial L}{\partial r^{(t)}} = \frac{\partial L}{\partial y^{(t)}}\frac{\partial y^{(t)}}{\partial r^{(t)}} = \frac{\partial L}{\partial y^{(t)}} \phi'(r^{(t)})\\ \frac{\partial L}{\partial h^{(t)}} = \frac{\partial L}{\partial r^{(t)}} \frac{\partial r^{(t)}}{\partial h^{(t)}} + \frac{\partial L}{\partial z^{(t+1)}} \frac{\partial z^{(t+1)}}{\partial h^{(t)}} = \frac{\partial L}{\partial r^{(t)}} v + \frac{\partial L}{\partial z^{(t+1)}} w\\\frac{\partial L}{\partial z^{(t)}} = \frac{\partial L}{\partial h^{(t)}}\frac{\partial h^{(t)}}{\partial z^{(t)}} = \frac{\partial L}{\partial h^{(t)}}\phi'(z^{(t)})\] \[\frac{\partial L}{\partial u^{(t)}} = \frac{\partial L}{\partial z^{(t)}}\frac{\partial z^{(t)}}{\partial u^{(t)}} = \frac{\partial L}{\partial z^{(t)}}x^{(t)}\\ \therefore \frac{\partial L}{\partial u} = \sum_{t=1}^T {\frac{\partial L}{\partial u^{(t)}}} = \sum^T_{t=1}\frac{\partial L}{\partial z^{(t)}}x^{(t)}\] \[\frac{\partial L}{\partial v^{(t)}} = \frac{\partial L}{\partial r^{(t)}}\frac{\partial r^{(t)}}{\partial v^{(t)}} = \frac{\partial L}{\partial r^{(t)}}h^{(t)}\\\therefore \frac{\partial L}{\partial v} = \sum_{t=1}^T {\frac{\partial L}{\partial v^{(t)}}} =  \sum^T_{t=1}\frac{\partial L}{\partial r^{(t)}}h^{(t)}\] \[\frac{\partial L}{\partial w^{(t)}} = \frac{\partial L}{\partial z^{(t)}}\frac{\partial z^{(t)}}{\partial w^{(t)}} = \frac{\partial L}{\partial z^{(t)}}h^{(t+1)}\\ \therefore \frac{\partial L}{\partial w} = \sum_{t=1}^{T-1} {\frac{\partial L}{\partial z^{(t+1)}}} = \sum^{T-1}_{t=1}\frac{\partial L}{\partial z^{(t+1)}}h^{(t)} (\because number of w = T-1)\]
    • Gradient vanishing and exploding

      • RNN 구조에서 왜 gradient vanishing 혹은 exploding이 일어나는지 분석하기위해, input을 hidden state로 mapping하는 과정에서 얻어지는 error signal에 대해 backpropagation을 하는 과정을 살펴본다. (hidden state가 중점이므로 hidden state만을 이용한다고 가정한다.)

        rnn_9.PNG

        그렇다면 \(\frac{\partial L}{\partial h^{(t)}} = \frac{\partial L}{\partial z^{(t+1)}}w, \frac{\partial L}{\partial z^{(t)}} = \frac{\partial L}{\partial h^{(t)}}\phi'(z^{(t)})\)인 것을 확인할 수 있다.

        \[\frac{\partial L}{\partial h^{(1)}} = \frac{\partial L}{\partial h^{(T)}} \frac{\partial h^{(T)}}{\partial z^{(T)}} \frac{\partial z^{(T)}}{\partial h^{(T-1)}} ,...,\frac{\partial h^{(2)}}{\partial z^{(2)}} \frac{\partial z^{(2)}}{\partial h^{(1)}}\\ = w^{T-1}\phi'(z^{(T)})\phi'(z^{(T-1)}),...,\phi'(z^{(1)})\]

        이때, 만약 activation function \(\phi\)가 linear하다면, 상수로 나타낼 수 있고 이는 간략하게 \(\frac{\partial L}{\partial h^{(1)}} =w^{T-1}\)로 나타낼 수있다. \(w\)가 상수인 경우로 테스트를 해보면, T=50상황에서, 1보다 0.1만 크거나 작아도 \(\frac{\partial L}{\partial h^{(1)}} =(1.1)^{50}=117.4,\frac{\partial L}{\partial h^{(1)}} =(0.9)^{50}=0.00515\)으로 나타난다. \(W\)가 matrix인 경우에도, matrix자체가 linear transform이므로, eigenvalue가 eigenvector를 선형변환후에 얼마나 stretch or squish하냐의 의미가 있으므로 이 값이 위에서 본 것처럼 조금만 차이나도 explode하거나 vanishing하는 현상이 일어난다. non-linear function이라면(sigmoid나 tanh같은), 함숫값이 커지면, clipping은 되지만 saturated되기 때문에, gradient가 vanishing하는 현상이 일어난다.

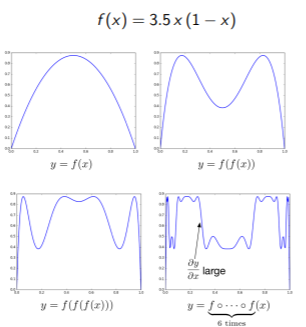
      • 함수적 관점에서 보았을 때, RNN computation은 function recursive하게 해석할 수 있다. 예를들어 나타내자면, \(h^{(t)} = f(x^{(t)},h^{(t-1)})\)일 때, \(h^{(4)} = f(f(f(h^{(1)},x^{(2)}),x^{(3)},x^{(4)})\)로 나타낼 수 있다. 이는 function \(f\)를 recursive하게 iteration한 결과이다. 이번엔 function \(f\)가 \(f(x)=3.5x(1-x)\)인 경우를 예로 들자면,

        rnn_10.PNG

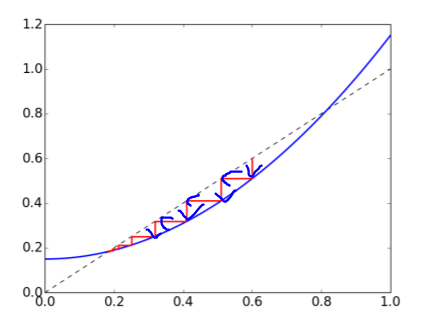
        다음과 같다. 한눈에 보기에도 함수가 합성될수록, 함수가 복잡해지고, 위 그림의 범위내 최대 기울기가 증가하는것을 볼 수 있다. 또 이런 재밌는 예로 Mandelbrot set이 있다. 이는 복소수 \(z_n =z^2_{n-1}+c\)로 나타낼 수 있는데, \(c\)의 값에 따라, n을 증가시킬때, \(z_t\)값이 수렴하는 집합들을 나타낸 것이다. 간단히 하기 위해 이중에서 단조증가하는 예를 가져오면 \(x_n = x^2_{n-1}+0.15\)를 예로 들 수 있다. 이는

        rnn_11.PNG

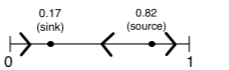
        다음 그림처럼 나타나고, 0.17 주변에서 그값으로 n이 커질수록 수렴해가고, 0.82 근처에서 항상 좌우로 다른값으로 이동하는 것을 볼 수 있다.

        rnn_12.PNG

        이는 0.17같은 fixed point를 sink혹은 attractor라고 하고, 0.82같은 fixed point를 source라고 한다. 좀더 분석해보면, fixed point에서의 derivates가 1보다 작으면 sink가 되고 , 1보다 크면 source가 된다.

        RNN연산이 다음과 같이 어떤 역학계에 속해있다고 할때, 다양한 attractors가 있을 것이고, 어느 attractor의 영역내에서 값이 존재했을 때, 이는 결국 attractor 근처에선 jacobian이 0에 가깝고 결국 연산을 통해서 그 영역 내의 attractor로 수렴할 것이다. 만약 영역의 경계선에서는 조금 벗어나면 바로 다른 attractor에게 끌려갈 것이다.

        rnn_13.PNG

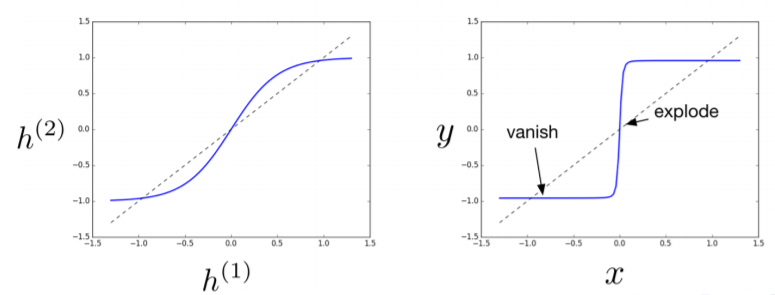
        위에 내용을 다음과 같은 activation function으로 tanh를 사용하는 RNN 구조에서 좀더 구체적으로 하자면, 어느지점에서 exploding을하고, 어디서 vanishing을 하는지 알 수 있다.

        rnn_14.PNG

        rnn_15.PNG

        이러한 형태의 output은 결국 RNN내의 parameter들에게 loss에 대한 정확한 error signal을 전달하지 못하게 된다.

    • 해결 방법
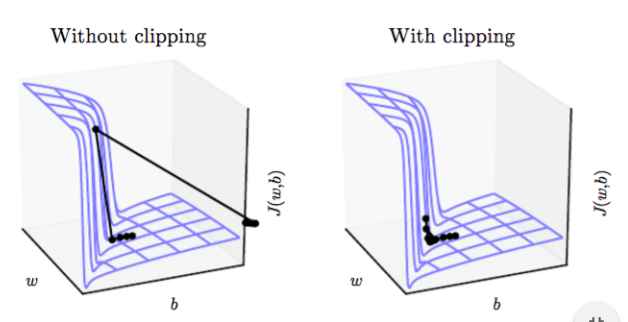
      • Gradient clipping

        • gradient update시 \(g \leftarrow \frac{\eta g}{\left \| g\right \|}\)를 통해, update하려는 gradient를 normalization을 해 진행한다. 이 biased gradient update는 cost function의 정확한 signal은 아니지만, update가 stable하도록 돕기 때문에 유의미 하다.

          rnn_16.PNG

      • Input Reversal

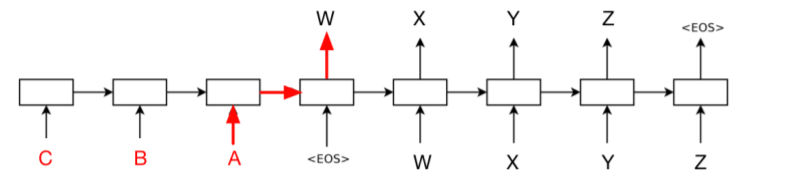
        • Sequence-to-Sequence 구조에서, Input의 sequence와 Output의 Sequence가 유사한 경우, Input sequence를 뒤집어서 encoding하는 것도 방법일 수 있다.

          rnn_17.PNG

          다음과 같이, Input sequence의 시작점이 Output sequence의 시작점과 1-step차이이기 때문에, 모든 sequence의 거리가 먼것보다 시작점위치가 가깝게 하여 학습하는 것이 유의미하다고 판단한 방법이다. 다만 평균 거리는 똑같아서 실제 이렇게 학습하는 것은 사실 최근에 본적은 없다.

      • Identity Initialization
        • 함수적 관점에서 봤을 때 문제점이, recursive하게 복잡한 함수가 합성될 때, gradient를 구하는 것이 어려워지는 것을 보았는데, 이를 identity activation function을 이용하면 해소될 수 있음을 짐작할 수 있다. 그래서 activation function에 ReLU를 사용하여, opimization을 진행했을 때, 더 좋은 결과를 얻은 실험들이 있다.
      • Long-Term Short-Term Memory(LSTM)

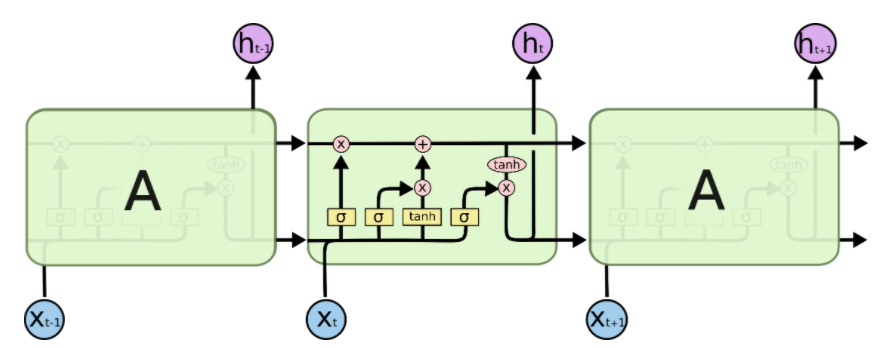
        • LSTM만 가지고 한 챕터를 쓸 수 있을 정도로 중요한 RNN의 진전인데, computation issue로 최대한 RNN을 안쓰려는 추세속에서도 써야한다면 LSTM or GRU을 사용하는 경향이 보인다. 여기서는 LSTM만 설명할 것인데, Long Term memory Cell이 추가되어, dribble된다. 그림으로 보자면 먼저 다음과 같다.

          rnn_18.PNG

          3개의 gate를 이해하는게 중요하다.

          • Forget gate
            • \(f_t = \sigma(w_{fh}h_{t-1} + w_{fx}x_t +b_f)\)로, input값과 이전의 hidden state로부터, 얼마나 값을 저장할지, 버릴지에 대해 결정한다. 그래서 sigmoid를 통해 0~1사이로 clipping되며, \(C_{t-1}\)과 element-wise 곱이 되어, 특정 dimension의 보존양으로 보면 된다. \(f_t \odot C_{t-1}\)
          • Input gate
            • \(i_t = \sigma(w_{ih}h_{t-1} + w_{ix}x_t + b_i)\)를 통해, Input을 cell에 얼마나 반영시킬지 양(가중치로 해석할수있는)을 계산해낸다.
            • \(\tilde{C_t} = tanh(W_{ch}h_{t-1}+ w_{cx}x_t+b_c)\)를 통해, Input을 cell에 얼마나 반영 시킬지 값(-1~1로 clipping된)을 계산해낸다.
            • 그리고 \(i_t\)와 \(\tilde{C}\)의 element-wise 곱을 forget gate에서 구한 \(f_t \odot C_{t-1}\)와 더한것이 현재 cell state가 된다. → \(C_t = f_t \odot C_{t-1} + i \odot \tilde{C_t}\)
          • Output gate
            • \[o_t = \sigma(w_{oh}h_{t-1} + w_{ox}x_t + b_o)\]
            • \(h_t = o_t\odot tanh(C_t)\)의 연산을 통해, 시점 t에서의 hidden state \(h_t\)를 만든다.
          • 개인적 사견으로 cell과 hidden state는 둘다 tanh와 sigmoid로 normalize된 값과 attention weight처럼 내부 parameter를 조절하고 있다.
  3. Next Step
    • ..
  4. References