Cramer’s rule, explained geometrically

What to learn

  • Understand Cramer’s rule by geometrically

    Description

  • Gaussian elimination is always fast. But understanding cramer’s rule geometrically will help to stretch out our linear algebra skill.

  • About linear transformation \(T\),

    \[\begin{bmatrix} x \\ y \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 0 \end{bmatrix} \neq T\left ( \begin{bmatrix} x \\ y \end{bmatrix} \right) \cdot T \left ( \begin{bmatrix} 1 \\ 0 \end{bmatrix}\right)\]

    But, if \(T\) is orthonormal(orthogonal and unit), then

    \[\begin{bmatrix} x \\ y \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 0 \end{bmatrix} = T\left ( \begin{bmatrix} x \\ y \end{bmatrix} \right) \cdot T \left ( \begin{bmatrix} 1 \\ 0 \end{bmatrix}\right)\]

    and, Any orthonormal linear transformation \(A\),

    \[\begin{bmatrix} a & b \\c&d \end{bmatrix} \begin{bmatrix} x\\y \end{bmatrix} = \begin{bmatrix} e\\f \end{bmatrix}\]

    we can find misterious vector \(\vec{v}\) by inner dot

    \[x = \begin{bmatrix} e\\f \end{bmatrix}\begin{bmatrix} a\\b \end{bmatrix}, y = \begin{bmatrix} e\\f \end{bmatrix}\begin{bmatrix} b\\d \end{bmatrix}\]

    Because, basis of transformed \(\vec{x}\) is same as the result of inner dot \(\begin{bmatrix} e\\f \end{bmatrix}\) with new basis.

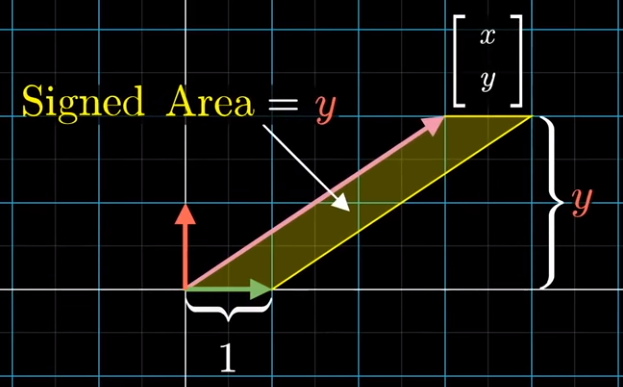
  • Yellow area is 1 * y

    linear_algebra_4.PNG

    Then, after transformated, we can calculate area of yellow area transformed by \(A\) is \(det(A)y\).

    • Because, it is linear transformation. \(1 \times y\) stretch out \(det(A) \times 1 \times y\)

    So, \(y = \frac{Area}{det(A)}\), Area is (landing vector \(\vec{v}\)) \(\cdot\)(transformed i hat). We can describe like this.

    \[y = \frac{Area}{det(A)} = \frac{\left( \begin{bmatrix} a & v_1 \\c&v_2 \end{bmatrix}\right )}{\left ( \begin{bmatrix} a & b \\c&d \end{bmatrix}\right )}\]

    And we can get x same as y.

    \[x = \frac{Area}{det(A)} = \frac{\left( \begin{bmatrix} v_1 & b \\v_2&d \end{bmatrix}\right )}{\left ( \begin{bmatrix} a & b \\c&d \end{bmatrix}\right )}\]

Next Step