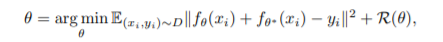- Abstract
- 이 논문은 agent의 쉬우면서도 오버헤드가 적은 exploration strategy에 대한 설명을 합니다. 이 때, exploration이 어떠한 intrinsic reward에 의해 이루어지는데, 이 reward(exploration bonus)는 논문 제목에서와 같이 random하게 initialize된 한 고정된 neural network의 forward pass한 값의 error입니다. 이 논문은 이를 통해 exploration이 문제가 됐던 atari games중에서 인간의 평균을 넘어서는 모습을 보입니다.
- Introduction
- RL의 발전은 굉장히 다양하면서도 어려운 문제들을 해결했고, 이러한 해결에는 병렬적으로 많은 양의 데이터를 사용함으로써 이루어졌습니다. 이 때, exploration strategy는 이전과 비교해서 확장성이 떨어지고, 효율적이지 못했습니다.
- 이 논문에서는 neural network가 이전에 방문했던 states에 대한 observation에서 낮은 prediction error를 보이는 점을 이용한 연구 방식에서 착안합니다. 그리하여 prediction error를 사용해
- 간단하고,
- high-dimension에서 잘 working하며,
- computation 측면에서 효율적인
방법을 제시합니다.
- 이전의 많은 연구자들이 이러한 방법에는 dynamics의 stochastic함에 의해 생기는 문제에 대해 지적하였습니다. 이러한 prediction error는 stochastic한 상황과 un-explorated한 상황에 대해 구별할 능력이 없습니다. 그렇기 때문에 의미없는 stochastic한 상황에 있어서도 intrinsic reward가 높게 부여될 수 밖에 없습니다.
- 그렇기 때문에, 여기서는 이를 해결하기 위해 이를 input을 deterministic하게 만드는 방법을 택했습니다.
-
Method
3.1 Exploration Bonuses
- Exploration bonuses는 exploration을 위해 reward 형태로 agent가 학습하는데 사용되는데, 기존의 \(r_t\)를 \(r_t=e_t+i_t\)로 시점 t에서의 extrinsic reward와 intrinsic reward형태로 나타낼 수 있습니다. 이 챕터에서는 이 exploration을 “잘”해내기 위한 previous works들을 소개하는데, count-based, pseudo-counts, 그리고 intrinsic reward를 사용한 이전의 연구들에 대해 흐름을 소개합니다.
3.2 Random Network Distillation
- 이번 챕터에서는 주요 아이디어와 함께 MNIST에서의 실험 결과를 얘기합니다. key idea만을 간략하게 설명하면, exploration bonus를 만들기 위한 network는 두 개 입니다.
- target network : fix(freeze)하고, 처음 initialized된 이후 weights이 바뀌지 않습니다. observation을 통해 정해진 output dimension의 vector를 만듭니다.
- predictor network : observation을 통해 정해진 output dimension의 vector를 만듭니다. 이 때 predictor network의 output과 target network의 mean squared error를 통해 predictor network가 학습됩니다.
3.2.1. Source of prediction errors
- prediction error는 다음과 같은 요소들에 의해 영향을 받습니다.
- Amount of training data : predictor가 자주 보지 못한 데이터일수록 prediction error가 높습니다.
- Stochasticity : dynamics가 stochastic할수록 prediction error가 높습니다.
- Model misspecification : observation을 나타내기 위한 중요한 정보량이 손실될수록, class가 target function의 complexity를 맞추기에 너무 제한된 경우 prediction error가 높습니다.
- Learning Dynamics : target function에 맞추기 위한 predictor의 학습이 실패했을 때 prediction error가 높습니다.
- 첫번째 요소가 우리가 원하는 prediction error지만, 실제로 이 네가지 요소들에 의해 prediction error가 발생됩니다.
- 두번째 요소는 동전 앞 뒷면 관측과 같이 stochastic한 결과를 얻을 때 발생하는 prediction error로, “noisy-TV”라는 문제에 빠지도록 유도합니다. 이를 기존의 intrinsic reward를 사용하는 방식이 효과적으로 해결하지 못했던 문제입니다. 이 논문은 이 2번과 3번의 문제를 효과적으로 해결하는데 기여합니다.
3.2.2. Relation to uncertainty quantification
-
RND에서의 prediction error는 Osband의 연구 중 불확실성의 양을 측정하는 방법과 관련되어 있습니다. 이번 챕터를 이해하기 위해서는 사실 bayesian rule과 함께 bayesian neural network를 함께 이해하고 있어야 쉽게 이해할 수 있습니다. 간단하게 설명을 하자면, 기존의 Neural entwork는 uncertainty에 대한 고려를 하지 않음이 자명하고(예를 들면, unseen data가 들어왔을 때, 어느 class의 값이 dominant함이 보일 수 있습니다. 하지만 그 output은 uncertainty가 높지만 이같은 점이 고려되지 않습니다.) 그로인해 uncertainty를 계산하자는 개념에서 Bayesian neural network를 통해 이제 특정 class에 대해 분포로 값을 추정할 수 있게 되었고, 이런 측면에서 uncertainty 문제가 RL에서도 똑같이 발생하므로 어떻게 이를 해결할까가 Osband의 연구였습니다. 그 연구에서 사용되는 방법이 다음의 (1)의 식과 유사한데, 먼저 식을 보겠습니다.
prior theta(weights로 일단 이해하고 이후에 prior, posterior등에 대해 좀더 깊게 찾아보시면 좋겠습니다.), mapping function f(neural network 정도로 생각하면 됩니다.) 를 가지고 untrainable한 network를 이용해 prior \(\theta^*\)를 함께 ensemble하여 posterior를 근사하는 과정입니다. 이 때, \(y_i\)가 0일 경우에 대해, 두 network가 unbiased되었다면, (mean이 같다면) 같은 loss function으로 볼 수 있습니다. 그렇기 때문에, distillation error는 zero function을 predicting하는 불확실성의 양을 측정하는 것과 같습니다.
3.3 Combining Intrinsic and Extrinsic Returns
- 다음으로, intrinsic reward와 extrinsic reward를 어떻게 결합하여 줄것인가에 대해 고민해 보아야 합니다. 또한, 이 intrinsic reward는 extrinsic reward가 한 episode내에서 일어난 reward에 대해 주어져야 하는 것이 기본적으로 맞지만, novel한 state는 episode를 넘어 다양하게 발생될 수 있습니다. 그렇기 때문에 이 논문에서는 non-episodic intrinsic reward, episodic extrinsic reward를 linear 결합으로 total reward를 만드는데, 이 성질이 다른 두 reward를 다루기 위해(approximation) 두 개의 value function을 사용하게 됩니다.
3.4 Reward and Observation Normalization
- 또한 intrinsic reward의 크기를 어떻게 조절할까에 대해 고민해보아야 하는데, 이를 intrinsic reward의 running estimation의 표준편차로 나눠서 조절합니다.
- target network또한 parameter가 계속 고정되어있기 때문에, target network에도 observation을 잘 normalization하여 넣어주어야 합니다. 그리하여 observation은 running mean으로 빼주고, running std로 나눈 뒤 -5~5로 clipping합니다. 이는 predictor와 target network, policy network에도 동일하게 적용됩니다.