한줄 리뷰 : background가 많이 필요한 논문이지만, 큰 틀은 Hindsight Experience Replay를 벗어나지 않기때문에 이를 이해하고 있으면 생각보다 쉬울 수 있습니다. 표기에 벡터등에 대한 bold 표기를 귀찮아서 안했으므로 논문과 대조해서 보셔야합니다.
A Generalized Algorithm for Multi-Objective Reinforcement Learning and Policy Adaptation
Abstract
이 논문은 multi-objective reinforcement learning(MORL)에서, 상대적인 objective들간의 선형적인 중요도(선호)에 대해 해결한 논문입니다. Agent는 multi-objective에 대해서 상대적인 중요도에 대해 알고있지 않습니다. 이는 유저의 reward shaping을 통해 어느정도 해결할 수 있지만, 다른 중요도에 따른 결과를 얻기 위해선 큰 소요가 발생하게 됩니다. 이 논문은 하나의 agent만으로 모든 중요도 공간을 탐색할 수 있는 알고리즘을 제시합니다.
Introduction
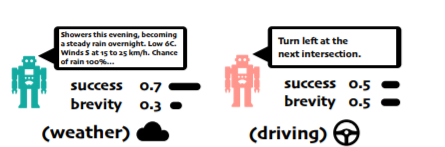
위의 그림을 보면, 일기 예보와 네비게이션같은 여러 경우에서 같은 objective의 틀을 가지고 있다고 해도, 그 기준이 다릅니다. 이런 상대적인 중요도는 이전엔 스칼라 값의 보상으로 결국 환경 설계자의 도메인 지식등에 크게 영향을 받았습니다. 이러한 제한은 특정 상황에 원하는 policy를 얻기위해 여러번 재설계를 해야하는 등 많은 소요를 발생시킵니다.
이에 대해 MORL은 두가지 장점이 있습니다.
- 첫째로, 여러 objectives를 합쳐서 의도치않은 방향의 학습이 이루어지는 경우를 줄일 수 있습니다.
- 둘째로, 중요도를 쉽게 변경하거나 다른 업무에 적용할 수 있습니다.
그리고 MORL은 두가지 전략을 통해 발전해왔습니다.
- 첫째로 하나의 objective로 변환해 사용하는 것인데, 이는 RL algorithm을 바로 적용하여 최적화시킬 수 있습니다. 하지만 이는 평균적인 objective에 대해서만 배우게되어 특정 중요도에 있는 optimal에 대해 배울 수가 없습니다.
- 두번째로, 전체의 optimal policy의 set을 계산하는 것인데, 이는 많은 계산량에 의해 scalability가 한계가 있습니다. 이후에 설명하겠지만, Pareto front를 표현하는게 domain의 사이즈가 커질수록 기하급수적으로 어려워지기 때문입니다.
이 논문은 하나의 policy network를 가지고, 중요도의 전체 space를 다루는 방법을 설명하는데, 이는 유저가 원하는 중요도에 대해 손쉽게 제공할 수 있도록 할 수 있음을 알 수 있습니다. 그래서 여기서는 두가지 MORL의 문제를 해결하는데,
- 첫째로, multi-objective에서의 Q-Learning MORL with linear preferences의 이론적인 수렴을 보입니다.
- 둘째로, MORL을 더 큰 영역으로 확장하기 위해 neural network의 효과적인 사용을 보입니다.
이 논문은 두가지의 핵심 아이디어가 있습니다.
- 첫째로, 중요도를 가지고 일반화하여 축소시킨 optimality operator가 유효했다는 점입니다.
- 둘째로, convex envelope형태의 Q-value를 중요도와 최적의 정책 사이에서 효과적으로 결합하게 됩니다.
여기서는 Hindsight Experience Replay와 homotopy optimization을 사용하고, 새로운 환경에 대해 어떻게 자동으로 중요도를 선정하는지 보입니다.
background
MOMDP는 다음과 같은 tuple로 나타낼 수 있습니다.
\[\langle \mathcal{S}, \mathcal{A}, \mathcal{P}, \Omega,f_{\Omega} \rangle\]순서대로
- state space, action space, transition distribution, vector reward function, space of preferences, preference function 인데, 주목할 점은, reward가 vector라는 점과 preference는 이전에 말하던 중요도(선호)를 가르킨다는 점입니다. preference function은 linear한 function으로 정의하며, 수식으로 정의하면, \(f_{\omega}(r(s,a)) = \omega^Tr(s,a)\) 로 정의할 수 있다. 당연하지만, 만약 \(\omega\)가 고정된다면, MOMDP는 MDP로 나타낼 수 있습니다. 한편으로, multi-objective에서 파레토 최적관련 개념이이 나오게 되는데, 이를 여기에 적용하면, 파레토 최적의 set을 구하면, 이 set내의 값들은 누적보상합이 더 나아질 수 없는 상태를 의미하게 됩니다. 이를 수식으로 나타내면 \(\mathcal{F}^* := \{\hat{r} | \nexists\hat{r}' \in \mathcal{F}^*\}\) 가 됩니다. \(\hat{r}\) 은 \(\hat{r} := \sum_t{\gamma^tr(s_t,a_t)}\) 입니다.(누적보상합)
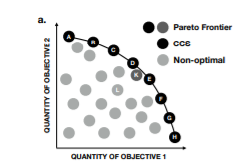
그러므로 우리는 가능한 모든 중요도 \(\Omega\) 에서 pareto frontier의 convex coverage set을 다음처럼 정의할 수 있습니다. (convex set은 간단히 두점을 이었을 때 그 선분위의 점들이 set에 포함되는 set을 나타냅니다.)
\(CCS := \{ \hat{r} \in \mathcal{F}^* \mid \exists \omega \in \Omega s.t. \omega^T\hat{r}\geq \omega^T\hat{r}', \forall\hat{r}' \in \mathcal{F}^* \}\) 로 나타냅니다. 그러므로 CCS내의 원소들은 어느 objective를 다른 objective의 안좋은 영향을 끼치지 않은 채로 optimize할수가 없다는 뜻입니다.
이는 그림과 같습니다.
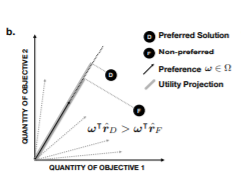
그리고 여기에, linear \(\omega\) 가 주어진다면, 가장 큰 projection값을 갖는 방향이 optimal solution이 될 것입니다.
이는 그림과 같습니다.
그리고 이 논문은 두개의 단계로 MORL을 진행합니다.
- Learning phase : 여기서는 agent가 CCS에서의 optimal policy \(\Pi_{\mathcal{L}}\) 를 배우게 됩니다. \(\pi\) 가 optimal policy \(\Pi_{\mathcal{L}}\) 에 속한다면, 어떤 \(\omega\) 에선 다른 어떤 policy \(\pi'\) 보다 가장 좋은 optimal임을 아래의 수식에서 볼 수 있습니다.
- Adaption phase : learning후에, 새로운 task를 받았을 때, unseen preference에 대해 어떻게 적용할지에 대한 파트입니다.
2.1 Related Work
Introduction에서 나왔던 내용을 좀더 자세하게 설명합니다.
- Multi-Objective RL
- Single-policy Method : objective에 대해 주어진 중요도에 대해 학습합니다. 그렇기 때문에 중요도가 주어지지 않았을 때, 동작할 수 없습니다.
- Multi-policy Method : 위에서 설명했던 Pareto frontier를 근사하기 위해서 policy에 대한 집합을 학습합니다. 이는 scale-up이 제한된다는 것을 말하고, 거기에 새로운 중요도에 대해 쉽게 적용할 수 있지 않습니다.
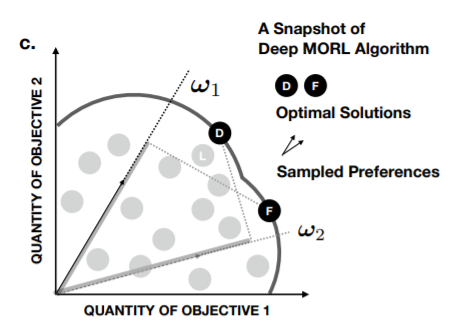
- Scalarized Q-Learning : 이는 중요도 벡터와 vector형식의 value function과의 inner product를 사용하는 Q-learning입니다. inner loop에서는 스칼라로 업데이트하지만 outer loop에서는 이러한 중요도를 찾기 위해 이런 방법을 사용합니다. 이전의 연구에서도 single neural network를 가지고 중요도에 대한 전체 space를 나타내도록 학습했던 시도가 있었는데, sample efficiency가 떨어졌고, sub-optimal을 피할 수 없었습니다. 이는 다음 그림에서 알 수 있습니다.
이전의 연구에서도 중요도와 잘못 매칭된 optimal solution들을 가지고도 학습을 할 수 있었으나, 한 선호도를 가지고 여러 optimal solution에 학습할 수 없었습니다. 이를 Hindsight Experience Replay의 방법을 차용하여서 한 sample로 sample efficiency를 높이면서, sub-optimal에서 벗어날 수 있도록 하였습니다.
이 논문의 contribution은 결국 세가지로 정리할 수 있습니다.
- 첫째로, 알고리즘 레벨에서 policy network를 업데이트하기위해, solution frontier의 convex envelope를 이용한 Q-learning을 진행합니다.
- 둘째로, 이론적인 레벨에서 value-based MORL 알고리즘을 소개하고, 수렴을 보입니다.
-
마지막으로 경험적인 수준에서 MORL의 성능을 테스트할 수 있는 기준과 벤치마크를 만들었습니다.
- Policy Adaption 이 논문의 policy adaption은 중요도 도출(preference elicitation) 혹은 역강화학습(inverse RL)과 관련이 있습니다. IRL에서는 expert의 도움으로 reward function을 배우거나, expert의 policy를 따라해 reward function를 배우는 형식입니다. IRL은 숨겨진 중요도가 고정됐거나 expert의 설명이 가능할때 유효한데, 여기서는 여러 다른 중요도가 사용되므로 더이상의 설명은 하지 않는다고 합니다.
Multi-objective RL with Envelope Value Update
이 섹션에서는 드디어 이 논문에서 제안하는 MORL 알고리즘 envelope Q-learning을 소개합니다. 키 아이디어는 vector화된 value function과 envelope update(파라미터를 업데이트할 때, frontier set의 convex envelope를 활용하는 방법입니다.)가 있고, 하나의 policy network를 이용하지만, 여러 중요도에 따른 policies set을 학습하는 것이기때문에 기존의 single-objective의 수렴성이 보장되지 않아 아래에서 알고리즘의 결과의 이론적인 분석을 먼저 진행합니다.
- Bellman operators Bellman operator T는 optimality filter(max) H 와 함께 다음과 같이 정의됩니다. \(TQ(s,a) := r(s,a) + \gamma \mathbb{E}_{s'~\mathcal{P}(\cdot \mid s,a)}(HQ)(s')\)
여기서 multi-objective q-learning은 아래와 같이 나타낼 수 있다.
\[\mathcal{T}Q(s,a,\omega) := r(s,a) + \gamma \mathbb{E}_{s' \sim \mathcal{P}(\cdot \mid s,a)}(\mathcal{H}Q)(s',\omega)]\]\(\mathcal{T}\)는 multi-objective optimality operator로 single-objective에서의 Bellman operator T와 같은 역할을 하는데 달라진 것은 \(mathcal{H}\)가 solution frontier set의 convex envelope에서 주어진 중요도 w와 주어진 state s에 대해 optimize를 한다는 점입니다.
Theorem 1
\(Q^*(s,a,\omega) = arg_Q \sup_{\pi \in \Pi}\omega^T \mathbb{E}_{\tau~(\mathcal{P},\pi) \mid s_0=s,a_0=a}[\sum^{\infty}_{t=0}\gamma^tr(s_t,a_t)]\)
으로, operator \(\mathcal{T}\) 는 value space에서 Fix된 하나의 point로 나타난다.
Theorem 2
Theorem 3
Learning Algorithm
전체 space를 \(\Omega\)로 두었을 때, \(\mathcal{Q} \subseteq (\Omega \rightarrow \mathcal{R}^m)^{\mathcal{S} \times \mathcal{A}}\) 로 나타낼 수 있다. 이는 m개의 중요도를 가짐을 의미하고, input으로 state와 , m-dim의 \(\omega\)가 들어간다. output으로는 원래 Action의 dimension의 Q값이 나오는게 보통 Q-learning방식인데, 여기서 \(\mathcal{A} \times m\) 의 vectorized q-value가 나오는게 특이점입니다.
reward도 그에 맞게 Objective마다의 reward를 발생시켜야하므로 같은 차원입니다.
loss는 두가지로 구성되는데,
\(L^A(\theta) = \mathbb{E}_{s,a,\omega}[\mid \mid y - Q(s,a,\omega;\theta) \mid \mid ^2_2], y = \mathbb{E}_{s'}[r + \gamma arg_Q max_{a,\omega'}\omega^TQ(s',a,\omega';\theta_k)]\) 로 Q-learning의 틀과 같다. loss를 이 하나만 쓰기에는 적용이 어려울 수 있는데 이는, optimal frontier가 너무 많은 discrete solution을 가져, loss function이 너무 non-smooth해 질 수 있기 때문에, 추가로 \(L^B(\theta) = \mathbb{E}_{s,a,\omega}[\mid \omega^Ty - \omega^TQ(s,a,\omega;\theta) \mid]\)
loss를 추가합니다. 이를
\(L(\theta) = (1- \lambda) \cdot L^A(\theta) + \lambda \cdot L^B(\theta)\)로, \(lambda\) 값을 천천히 증가시켜 처음엔 실제 total reward와 근사하고 점점 활용하기 좋게 만드는 형태로, 위에서 언급했던 homotopy optimization이라고 불리는 방법입니다.
loss function에는 \(\omega\) 에 대한 loss 가있는데, 이는 중요도에 대해 random sampling을 해서 얻게되지만, transition에서는 분리되어있기 때문에, sample efficiency 를 높이고, 이는 HER의 algorithm과 비슷한 형태를 띄고 있습니다. 그리고, \(\mathcal{H}\)를 전체 \(\mathcal{Q}\)에 대고 하기는 어려우니 minibatch에서 업데이트를 진행합니다.
Policy Adaption
중요도 \(\omega\)를 mltivariable Gaussian distribution에서의 sampling을 통해 policy model을 fix한뒤, argmax를 찾는 방법으로 새 테스크에 맞는 중요도를 적용시킬 수있다는 내용입니다.