Solving NP-hard Problems on Graphs with Extended AlphaGo Zero

Abstract

  • Graph neural network와 MCTS의 결합을 통해 Combinatorial Problem을 해결함을 보입니다. 이 때, 학습 방법으로 AlphaGo Zero를 변형한 CombOpt Zero를 소개합니다.

Introduction

  • 논문 전반으로 S2V와 많이 비교합니다. 이는 GNN과 greedy selection을 통해 dataset없이 학습이 가능했지만, 실제로 다른 특성을 가진 graph에 대해 성능이 좋지 않음을 확인했습니다. 이를 Q-learning의 exploration의 한계로 보았습니다.
  • 그렇기 때문에 Q-learning을 CombOpt Zero로 대체합니다. 이는 두 플레이어로 이루어진 게임에 제한되었는데 이를 sampling과 간단한 reward normalization을 통해 해결합니다.

Preliminary

  1. Notation
    • 논문의 graph \(G=(V,E)\)는 undirected, unlabelled graph를 사용합니다. \(V\)와 \(E\)는 vertices와 edges를 나타냅니다. \(V(G)\)는 graph의 vertices set을 의미합니다. \(\mathcal{N}(x)\)는 node \(x\)에 대한 한 edge로 연결된 neighbors를 의미하고, node set \(S\)에 대해 \(\mathcal{N}(S) = \bigcup_{x \in S} \mathcal{N}(x)\)와 같이 표현합니다. \(\boldsymbol{p}\)와 \(\boldsymbol{\pi}\)는 모두 vector이므로 bold체로 표기합니다.
  2. Machine Learning for Combinatorial Optimization
  3. AlphaGo Zero
    • AlphaGo Zero는 바둑에서 인간을 압도한 RL algorithm입니다. 이는 RL을 통해 parameter \(\theta\)의 neural network \(f_\theta\)를 학습시킵니다. state에 대해 network는 action에대한 distribution vector \(\boldsymbol{p}\)과 state value \(v, v\in [-1,1]\)를 output으로 가집니다.
    • AlphaGo Zero는 self-play를 통해 network를 update하는데, 이는 Monte Carlo Tree Search(MCTS)의 special version입니다. network는 MCTS로 얻은 \(\boldsymbol{\pi}\)와 \(\boldsymbol{p}\)가 같아지도록 cross-entropy를 최소화하고, value estimation \(v\)와 실제 self play를 통해 얻은 \(z\)의 l2-loss를 최소화하도록 합니다. 이를 regularization term과 함께 loss로 나타내면 다음과 같습니다.
\[\mathcal{L} = (z-v)^2 + \mathrm{CrossEntropy}(\boldsymbol{p},\boldsymbol{\pi}) + c_{\mathrm{reg}} \Vert\theta \Vert^2_2\]

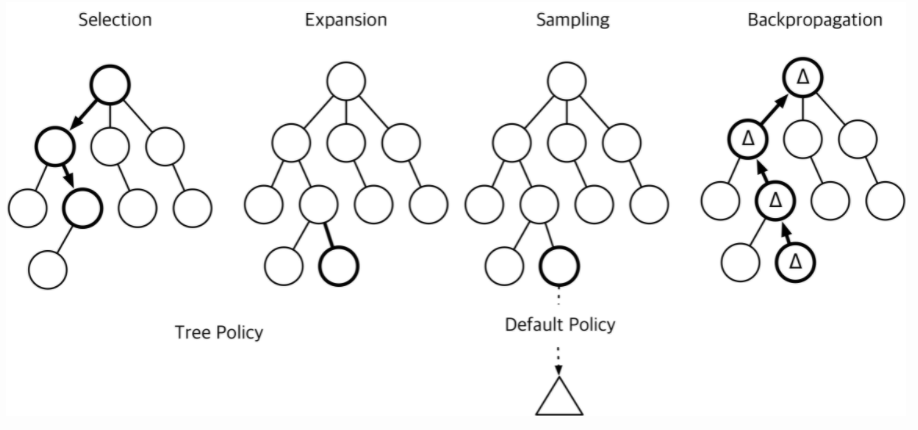
  • MCTS는 tree형식의 데이터에서 heuristic search를 위한 algorithm으로, root로 부터 다음과 같이 spanning 됩니다.

    alphago_zero_tsp

    이 때, edge는 다음과 같은 4가지 정보를 가지고 있습니다.

    \[(N(s,a),W(s,a),Q(s,a),P(s,a)) \cdots (2)\]
  • \(N(s,a)\)는 edge를 얼마나 방문했는지를 나타냅니다.
  • \(W(s,a)\)는 총 action value를 나타냅니다.
  • \(Q(s,a)\)는 평균 action value를 나타냅니다. \(\frac{W(s,a)}{N(s,a)}\)를 통해 나타낼 수 있습니다.
  • \(P(s,a)\)는 기존의 probability를 나타냅니다.

AlphaGo Zero는 그림의 세 번째 Sampling을 network prediction만을 이용하므로 이를 나타내면 다음과 같습니다.(하지만 여기선 sampling을 통해 random action에 대한 평균과 표준편차를 구하긴합니다.)

  • selection

    • root로 부터 다음의 upper confidence bound(UCB)를 maximize하는 Q를 선택합니다.

      \[Q(s,a) + c_{\mathrm{puct}}P(s,a)\frac{\sqrt{\sum_{a'}N(s,a')}}{1+N(s,a)} \cdots(3)\]

      이는 기존의 UCB에서 prior probability를 이용해 exploration을 좀 더 기존에 좋았던 방향으로 진행할 수 있도록 합니다.(worst case에 penalty를 주는 것과 같습니다.)

  • Expansion
    • 선택된 edge에 대해 unexplored node \(s\)를 추가하고, network를 통해 edge weights들을 initialize합니다.
  • Backup

    • edge를 traverse하며 방문한 edge value를 update합니다. \(Q\)는 각 edge의 총 가본 횟수와 도착한 node의 state에 대한 evaluation의 평균을 이용해 계산합니다.

      \[Q(s,a) = \frac{1}{N(s,a)}\sum_{s' \vert s,a →s'}v_{s'}\]

      MCTS의 \(\boldsymbol{\pi}\)는 temberature과 함께 가본 횟수에 의해 정의됩니다.

      \[\boldsymbol{\pi}_a = \frac{N(s_0,a)^{1/\tau}}{\sum_bN(s_0,b)^{1/\tau}}\]
  1. Graph Neural Network
    • GNN은 input을 graph로 받을 때 사용하는 neural network입니다.
    • structure2vec
      • 기존에 설명했으므로 생략합니다.
    • Graph Convolutional Network
\[H^{(l+1)} = \sigma(\hat{D}^{-1/2}\hat{A}\hat{D}^{-1/2}H^{(l)}\theta^{(l)})\]
  • 그래프의 인접행렬 \(A\)에 대해 \(\tilde{A} = A + I_n\)이고, \(D\)는 각 node의 degree를 나타내는 행렬일 때, \(\tilde{D}^{-1/2}\tilde{A}\tilde{D}^{-1/2}\)는 \(A\)를 정규화시킵니다. 그리고 이전의 hidden \(H^{(l)}\)를 곱하는 것은 각 노드의 hidden을 다음 neighbors의 hidden로 전달하는 것과 같습니다. 이 때 trainable matrix \({\theta^{(l)}}\)를 곱한뒤 마지막으로, non linearity를 더해 다음 \(H^{(l+1)}\)을 recursive하게 만듭니다.
  • Graph Isomorphism Network

    • aggregation, readout이 injective function이어야하기 때문에 neighbors와 자신 모두 더한 뒤 \(\hat{A}\)를 곱해 MLP를 통과합니다. 마지막으로 모든 MLP layer를 concatenate한 output을 사용하는데, 이를 나타내면 다음과 같습니다.

      \[H^{(l+1)} = \mathrm{MLP}^{(l)}(\tilde{A}H^{(l)}), \ y_v = \mathrm{MLP(CONCAT}(H^{(l)}_v \vert l = 0,1, \cdots,L))\]
  • 2-IGN+
    • 너무 길어지는 것 같아서 생략합니다.
  1. NP-hard Problems on Graphs
    • Minimum Vertex Cover
    • 모든 edge를 포함하는 nodes의 subset \(V' \subset V\)가 가장 작도록 하는 문제입니다. - Max Cut
    • cut set \(C \subset E\)의 size를 최대화하여 node의 subset \(V'\)을 만드는 문제입니다. - Maximum Clique
    • 모든 node가 연결된 node의 subset \(V' \subset V\)를 최대화 하는 문제입니다.

Method

이번 section은 CombOpt Zero를 통해 Graph combinatorial optimization problem을 해결하기 위한 방법을 설명합니다.

  1. Reduction to MDP
    • AlphaGo Zero의 method를 combinatorial optimization에 적용하기 위해서 graph problems을 MDP로 정의해야합니다. deterministic MDP는 다음에 의해 정의됩니다.
\[(S,A_s,T,R)\]

\(S\)는 states의 set, \(A_s\)는 state \(s\)로부터의 action set, transition probability \(T :S \times A_s →S\), reward \(R :S \times A_s → \mathbb{R}\) 로 정의합니다. 이 때, 각 state \(s\in S\)에 대해 label \(d\)가 붙습니다. labeling을 위한 function \(d : V →L\)에 대해각 state는 \(s = (G,d), \ G=(V,E)\)로 나타냅니다.

각 문제마다 마지막 state \(S_{\mathrm{end}}\)가 존재하고, 각 state \(s\)로부터 \(S_{\mathrm{end}}\)가 나올 때까지 action과 transition probability function를 통해 반복하게 됩니다. 이를 통해 state과 action sequence를 얻을 수 있고 이를 trajectory라고 합니다. 이를 통해 trajectory의 reward \(\sum^{N-1}_{n=0}R(s_n,a_n)\)를 구할 수 있고, \(r^*(s)\)는 state \(s\)로 부터 얻을 수 있는 최고의 optimal reward sum입니다. \(\mathrm{Init}\)은 input graph로부터 문제를 풀기 위한 state로 변환해주는 function로 사용됩니다. 이 때 목표는 주어진 graph \(G_0\)로부터 \(r^*(\mathrm{Init}(G_0))\)를 얻는 것 입니다.

  • Maximum Vertex Cover
    • label이 필요하지 않는 문제입니다. 그렇기 때문에 \(d\)는 constant function으로 두고 사용합니다. action은 한 node를 선택하는 것으로, 최대한 빠른 step안에 모든 node가 cover되도록 reward \(R(s,x) = -1\)을 설정합니다.

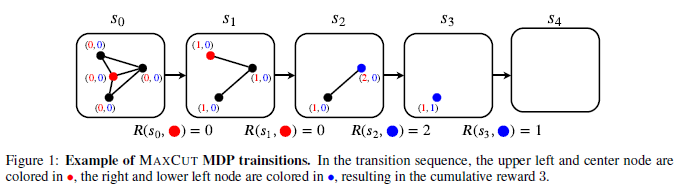
  • Max Cut

    alphago_zero_tsp

    • 각 action마다 node를 0이나 1로(파란색, 빨간색) 색칠합니다. 그리고 그 노드를 제거하면서 얼마나 많은 인접한 색색의 노드가 제거되었는지를 저장합니다. \(A_s = \{ (x,c) \vert x \in V, c \in \{1,2\} \}\)는 nodes에 색칠할 수 있는 set을 나타내고, \((x,c)\)는 node를 color c로 색칠하는 것을 의미합니다. \(L = \mathbb{N}^2\)는 각 adjacent nodes가 각 색에 의해 몇 회 색칠됐는지를 나타냅니다. \(R(s,(x,c))\)는 \((3-c)\mathrm{-th}\)에 대해 c가 1이면 2, c가 2이면 1의 \(d(x)\)값입니다.(색칠된 색의 반대 dimension을 고른 값)
  • Maximum Clique
    • 비슷하므로 생략합니다.
  1. Ideas for CombOpt Zero
    • Combinatorial Optimization vs. Go
    • AlphaGo Zero를 MDP formulation에 적용할 때 두가지 바둑과는 다른 점이 있습니다. 첫째로, 바둑은 고정된 input size를 가지나, combinatorial problem은 대체로 dynamic합니다. 그렇기 때문에 GNN을 통해 이를 해결합니다. 둘째로, 결과가 단순화되지 않습니다. 바둑은 승리하거나 비기거나 지는 경우로 나뉘는데 combinatorial problem은 그렇지 않습니다. 바둑처럼 \([-1,1]\)의 범위에서 큰 value를 가질수록 이길확률이 크다는 것을 따라서 만들 수 있지만, graph size가 커질수록, trajectory length가 길어지게되고, cumulative reward가 높다면, (3)의 첫 번째 term이 dominent해지게 되므로 탐색이 제대로 이루어지지 않습니다. 여기서는 normalization technic을 사용하여 이를 해결합니다.

    • 먼저 AlphaGo Zero의 network \(f_\theta(s) = (\boldsymbol{p},v)\)에서 value를 각 action에 대한 value로 만들어 state action value형태로 만듭니다. 이는 다음과 같이 표현합니다.

      \[f_\theta(s)= (\boldsymbol{p},\boldsymbol{v})\]

      이 떄 \(v_a\)는 state \(s\)에서 action \(a\)를 취했을 때의 normalized reward를 predict한 값으로 이 state에서 취한 action이 다른 random action보다 얼마나 좋은지를 나타내게 됩니다. \(v_a\)는 다음을 예측하도록 학습됩니다.(state \(s\)에서 action \(a\)로 인한 reward와 이후의 optimal reward를 normalization한 것)

      \[(R(s,a)+r^*(T(s,a)) - \mu_s) / \sigma_s\]

      이를 이용해 다시 unnormalized value에 대해 restoring할 수 있습니다.

      \[r_{\mathrm{estim}}(s)\left\{\begin{matrix}0\ \ \ \ \ \ (s \in S_{\mathrm{end}})\\ \mu_s + \sigma_s \cdot (\max_{a\in{A_s}}{v}_a)\ \ (\mathrm{otherwise})\end{matrix}\right.\]

      이리하여 \(W(s,a)\)와 \(Q(s,a)\)는 normalized된 value를 E가지게 됩니다.

  • Reward Normalization Technique
    • 이렇게 normalization을 하여서 (3)의 첫번째 term이 dominent해지는 현상에 대해 완화시킬 수 있게 되었습니다. 3. Algorithms
  • MCTS Tree Structure
    • Alphago Zero처럼 각 edge에 (2)의 정보를 가지고 있습니다. 추가적으로 node는 \((\mu_s,\sigma_s)\)의 tuple을 가집니다.

  • MCTS

    alphago_zero_tsp

    pseudo code는 다음과 같습니다. graph의 특성상 action space가 states에 따라 dynamic하므로 action space의 \(c_{\mathrm{iter}}\)에 비례하게 iteration할 수 있게 합니다. 또한 root의 prior probability는 Dirichlet noise를 넣어 explore을 촉진합니다.

    이후 selection과 expand, backup을 하는데, backup쪽만 살펴보겠습니다. \(f_\theta\)를 통해서 normalized state value를 얻은 다음 이를 random sampling을 통해 얻은 mean과 standard deviation을 통해 reward를 계속해서 normalization합니다. 그리하여 \(W(s,a)\)와 \(Q(s,a)\)는 모두 normalization된 값을 가지게 됩니다. 그리고 MCTS \(\boldsymbol{\pi}\)를 output으로 가집니다.

  • Training
    • CombOpt Zero의 학습은 세가지 구성요소로 이루어져있습니다.

      • data generators

        alphago_zero_tsp

        self-play records를 randomly generated graph로부터 계속해서 만듭니다. 이는 MCTS policy \(\boldsymbol{\pi}\)로 부터 생성된 trajectory로 볼 수 있습니다.

      • learners

        • 랜덤하게 sampling한 records로부터 다음과 같이(AlphaGo Zero의 loss와 같은) loss를 계산합니다.

          \[\mathcal{L} = (z'- v_a)^2 + \mathrm{CrossEntropy}(\boldsymbol{p},\boldsymbol{\pi}) + c_\mathrm{reg} \Vert \theta \Vert ^2_2\]
      • model evaluators
        • AlphaGo Zero처럼 두 플레이어 간의 winning rate를 구할 수 없으므로, random graph를 생성하고 mean performance를 측정하는 파트입니다.

References