Learning to Solve Combinatorial Optimization Problems on Real-World Graphs in Linear Time 논문 리뷰 및 설명

Learning to Solve Combinatorial Optimization Problems on Real-World Graphs in Linear Time

Abstract

• 이 논문에서는 graph combinatorial optimization problem에 대해 RL과 graph neural network을 결합해 해결하였습니다. 이 때, optimality gap이 1과 가까우면서도 linear running time을 가지며 generalization이 잘 되는 방법을 제시합니다.

Introduction

• 본 연구는 다음과 같은 두 가지 결과들에 영향을 받았습니다.
  • GNN 학습이 dynamic programming과 같고, polynomial time complexity를 가지는 algorithm을 묘사하는데 사용될 수 있다.(Appendix A.1을 보시는걸 추천합니다.)
  • GNN을 이용한 RL은 np-hard combinatorial optimization problems의 근사해를 찾는데 사용될 수 있다.
• 기존의 combinatorial problem을 풀기위한 GNN과 RL의 결합은 한 문제에 대해서만 optimization이 되었습니다. 하지만 여기선 다양하게 generalization이 가능함을 보입니다.
• contribution은 다음과 같습니다.
  1. Linear running time complexity with optimality gaps close to 1.
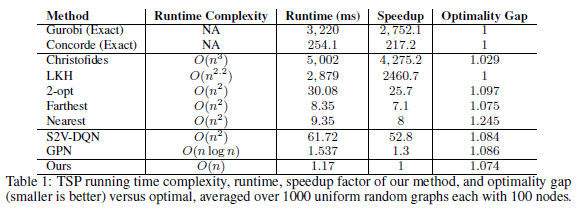
     • 본문 algorithm의 running time은 \(O(n+m)\)로, node와 edge에 linear합니다. 이전 논문들의 성능과 running time에 따른 table은 다음과 같습니다.
     • (optimality gap이 본문의 설명이 안나와있는데, 아마 \(\frac{\mathrm{result \ cost}}{\mathrm{optimal \ cost}}\)정도로 예상합니다.)

     

  2. Generalization on graphs
     • 1) 작은 graph부터 큰 graph까지, 2)다양한 graph 생성 방식에 따른, 3)random graph에서 실제 tsp 문제에 적용에도 잘 generalization됨을 보입니다.
  3. A unified framework for solving any combinatorial optimization problem over graphs
     • line graph를 통해서 node action과 edge action에 모두 적용할 수 있음을 보입니다.

Unified Framework

• graph \(\mathcal{G}\)는 vertices, edges, weights로 이루어졌습니다. \(\mathcal{G} = (V,E,W),\ V = \{1,..,n \}\), edges \(e_{ij}\)는 \(w_{ij} = w_{ji}\)인 undirected edge이며, \(\vert V \vert, \vert E \vert\) 모두 vertices와 edges의 개수를 의미합니다. \(\mathcal{N}(i)\)는 node \(i\)에 대한 neighboring nodes입니다.

• Line graph

  

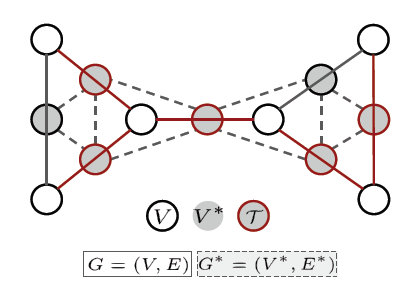
• 그림과 같이 원래 graph의 edges를 nodes로, nodes를 edges로 변환한 graph입니다. 이 line graph는 다음과 같이 정의합니다.

  \[\mathcal{G}^* = (V^*,E^*,W^*), \ V^* = E\]

  이는 기존 graph의 edges가 line graph에서는 vertices가 됩니다. weights또한 edges weights가 node의 weights가 됨을 알 수 있습니다. 이 연산은 edges도 nodes와 같이 action으로 사용하기 위한 변환입니다.

• Graph generation
  • Minimum Spanning Tree(MST)와 Single-Source Shortest Paths(SSP)를 학습하기 위해서 다섯가지의 random graph 생성방식을 사용합니다. TSP와 VRP을 학습하기 위해서도 random nodes를 만듭니다.

1. Problems over Graphs
   • Minimum Spanning Tree(MST)
   • connected and undirected graph \(\mathcal{G} = (V,E,W)\)에서 모든 nodes를 포함하면서 edge weights는 최소화하는 tree \(\mathcal{T} = (V_\mathcal{T},E_{\mathcal{T}}), (\ V_\mathcal{T} = V,\ E_\mathcal{T} \subset E)\)를 찾는 것이 목적입니다. greedy algorithm으로는 time complexity가 \(O( \vert E \vert \log \vert V \vert )\)임이 알려져 있습니다. - Single-Source Shortest Paths(SSP)
   • connected and undirected graph \(\mathcal{G} = (V,E,W)\)에 대해 한 node로부터 시작해 모든 nodes에 도달하는 최단거리들을 구하는 문제로 Dijkstra algorithm은 heap을 사용해 \(O( \vert V \vert \log \vert V \vert + \vert E \vert )\)의 time complexity를 가지고 있음이 알려져 있습니다. - Traveling Salesman Problem(TSP)
   • graph \(\mathcal{G} = (V,E,W)\)에 대해, \(V\)가 cities를 나타내고, \(W\)가 city간의 거리를 나타낼 때, 처음 도시를 지나 모든 도시를 들러 다시 처음도시로 도착하는 문제로 다양한 solver들이 존재합니다. - Vehicle Routing Problem(VRP)
   • \(M\)개의 vehicles을 가지고 graph \(\mathcal{G} = (V,E)\) 에 대해서 optimal route를 찾는 문제입니다. 각 vehicles은 depot에서 시작해 각자 겹치지 않으면서 모든 도시를 방문한 후 다시 depot으로 돌아오게 됩니다. 이 때 optimal은 route의 가장 긴 길이를 minimize하게 됩니다. TSP는 VRP의 special case로 볼 수 있습니다.
2. Learning Graph Algoritmhs as Single Player Games

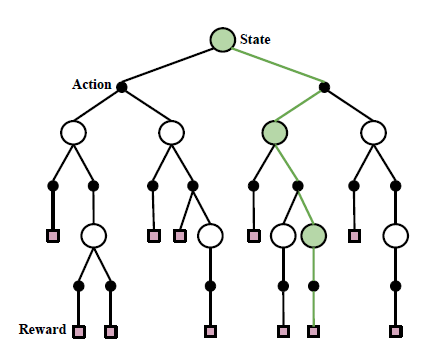
• 논문은 MCTS구조를 제안합니다. problem space를 search tree로, 각 leaves는 tree의 모든 가능한 해를 나타냅니다. 이 해를 찾는 과정은 학습된 neural network에 의해서 적절한 leaf를 찾는 과정입니다. initial state는 맨위의 root node로써, empty set이나 random state정도로 나타낼 수 있습니다. 이때 각 path는 edges(action)을 따라서 nodes(states)를 거쳐 leaf(reward)까지를 포함합니다. action은 node나 edge를 더하거나 뺄 수 있습니다. reward는 각 해의 적절성을 나타낼 수 있습니다. 다음의 table을 통해 각 state action reward를 어떻게 정의하였는지를 나타냅니다.

  

Methods

• 이제 state를 어떻게 embedding하고 action을 어떻게 뽑는지, 학습은 어떻게 하는지 설명합니다. 이 때, 이 framework은 다양한 문제에 general하게 적용가능하므로 다른 문제에 적용할 땐 objective function만 변경해주면 적용이 바로 가능합니다.

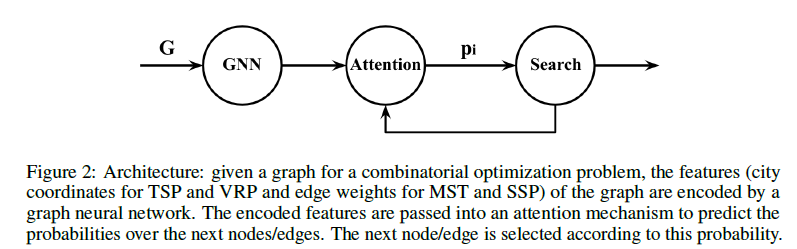
• 논문은 encoder와 decoder구조를 가지고있는데, encoder는 graph attention network(GAT), decoder는 attention model을 통해 iterative하게 action을 선택하게 됩니다. 이를 그림으로 나타내면 다음과 같습니다.

  

  MST와 SSP는 edge에 대한 연산을 하기 때문에 line graph를 계산해 사용합니다.

• Encoder
  • input은 graph \(\mathcal{G} = (V,E,W)\)로, 각 node에 대한 features \(\boldsymbol{v}\)는 다음과 같이 나타냅니다. \(\boldsymbol{v}_i \in \mathbb{R}^d, \ i \in \{1,...,n\},\ n = \vert V \vert\)

  • encoder의 각 layer는 다음과 같은 연산을 통해 계산됩니다.

    \[\boldsymbol{v}^l_i = \alpha_{ii}\Theta\boldsymbol{v}^{l-1}_i+ \sum_{j\in \mathcal{N}(i)}\alpha_{ij}\Theta\boldsymbol{v}^{l-1}_j\]

    이는 한 node의 feature \(\boldsymbol{v}^{l}_i\)에 대해 주변 neighbors와 함께 recursive하게 이뤄지는 attention연산임을 알 수 있습니다. \(\Theta\)는 trainable matrix이고, 각 neighbors에게 가중치를 부여하는 \(\alpha\)을 알아보자면, \(l\)번째 layer에 대해서 다음처럼 나타낼 수 있습니다.

    \[\alpha^l_{ij} = \frac{\exp(\sigma(z^{l^T}[\Theta^l\boldsymbol{v}^l_i,\Theta^l\boldsymbol{v}^l_j]))}{\sum_{k \in \mathcal{N}(i)}\exp(\sigma(z^{l^T}[\Theta^l\boldsymbol{v}^l_i,\Theta\boldsymbol{v}^l_k]))}\]

    \(z^l\)은 learnable vector, \(\sigma(\cdot)\)은 non-linearity를 위해 leaky ReLU를 사용합니다. 본 논문에서는 \(l = 1,2,3\)를 사용했는데, 마지막 layer L은 softmax를 통해 나타냅니다.

• Decoder

  • Decoder는 각 node feature \(\boldsymbol{v}_i \in \mathbb{R}^d\)에 대해 neighbors feature nodes \(\boldsymbol{v}_j,\ j \in \mathcal{N}(i)\)을 가지고 attention coefficient \(\alpha^{\mathrm{dec}}_{ij}\)를 구합니다.

    \[\alpha^\mathrm{dec}_{ij} = C \tanh((\Phi_1\boldsymbol{v}_i)^T(\Phi_2\boldsymbol{v}_j) / \sqrt{d_h})\] \[\mathrm{where}\ \ \Phi_1, \Phi_2 \in \mathbb{R}^{d_h \times d}, C \in \mathbb{R}\]

    이를 가지고, softmax를 통해 action의 distribution을 만들게 됩니다.

• Search
  • beam search나 neihborhood search, tree search를 사용할 수 있으나, probability를 통해 action을 선택합니다.

• Algorithm

  

• 지금까지 살펴본 문제들에 대해 general algorithm을 적자면, Input graph에 대해 line graph가 필요하면 계산하고, encoder로 encoding한 후, decoder로 action을 선택해 tree에 add합니다. training시엔 아래처럼 baseline을 넣은 REINFORCE algorithm을 통해 학습합니다.(baseline에 대한 특별한 언급은 없고 한 그래프에서 진행한다면 running estimation of mean정도로 사용해도 괜찮을 것 같습니다.)

1. Solutions
   • MST

   • graph \(\mathcal{G} = (V,E,W)\), \(W\)는 edge weights일 때, policy \(\pi\)는 edge를 선택해 더해야만 합니다. 이를 통해 tree를 정의하면, 다음과 같습니다. \(\mathcal{T} = (V,E_\pi,W_\pi),\ E_\pi \subset E,\ W_\pi \subset W\). reward는 다음과 같이 정의할 수 있습니다.

     \[r = -(I(\mathcal{T})+\sum_{e\in E_\pi}W(e))\]

     이 때, \(I\)는 indicator function으로, \(\mathcal{T}\)가 tree이면 0이되고, tree가 아니라면 매우 큰 값을 주어 invalid case에 대해 masking이 아닌 reward로 학습시킵니다. 결과적으로 agent는 low-weight edges와 tree에 대해 학습하게됩니다.

• TSP
  • 생략합니다.

References

• Learning to Solve Combinatorial Optimization Problems on Real-World Graphs in Linear Time

개인적으로 MCTS에 대해 조금 더 설명했으면 좋겠다는 생각에 MCTS에 관해 하나를 더 리뷰하려고합니다.