Reinforcement Learning for Solving the Vehicle Routing Problem 논문 리뷰 및 설명

Reinforcement Learning for Solving the Vehicle Routing Problem

Abstract

• Vechicle Routing Problem(VRP)을 해결하기 위한 end-to-end RL framework를 제시합니다. 이는 새로운 문제에 대해 재학습할 필요 없이 실시간으로 optimal solution에 가까운 결과를 도출합니다. 이 때, 기존 NCO를 VRP(VRP이 아니더라도)에서 적용할 때의 단점에 대해 설명합니다.

Introduction

• VRP는 Combinatorial Optimization Problem으로 수학과 컴퓨터 공학분야에서 오랜 세월 연구되어 왔습니다. 이는 주로 NP 문제로 알려져있지만, 해답을 찾을 수 있는 다양한 알고리즘들이 존재합니다. 하지만 정확하면서 빠른 해답을 찾는 것은 어렵습니다. 가장 간단한 형태의 VRP의 예로 하나의 vehicle은 여러 고객에게 아이템을 운반하고, 아이템이 떨어지면 다시 원점(depot)으로 돌아가 다시 물건을 실어와 운반합니다. 이 때 운송거리나 시간을 최소화 하는 것이 VRP의 한 예로 들 수 있습니다.
• 이러한 문제에 사람의 개입없이 새로운 알고리즘을 개발하는데에 neural network와 reinforcement learning의 도입은 필수불가결합니다. 그리하여 이번 연구에서는 RL을 통해 VRP를 해결할 수 있는 framework을 제시합니다.
• 학습은 한 data당 하나의 policy만을 학습시키는 것을 생각해 볼 수 있지만, agent에게 많은 데이터를 주어 MDP를 이해시키고 generalization하여 새로운 문제에서도 바로 inference할 수 있도록 만들어 inference 속도를 높이는 방법이 더욱 매력적입니다.
• 이 논문은 NCO로부터 영감을 받았습니다. 여기선 NCO의 framework를 VRP같은 문제로의 generalization을 다룹니다. 이때 NCO의 pointer network는 decoding시에 state의 static함을 가정하는데, VRP은 그렇지 않을 수 있습니다. 그렇기 때문에 Pointer network를 변형하여 RNN decoder엔 static element를 넣고, rnn의 output과 dynamic element의 embedding은 attention mechanism을 씀으로써 다음 action에 대한 distribution을 내놓게 됩니다.

Background

• Sequence-to-Sequence Models
  • Sequence-to-Sequence model은 한 sequence로부터 다른 sequence로의 mapping이 필요할 때 유용합니다. 이는 neural machine translation에서 오래 연구되었으며, 다양한 model을 만들었습니다. 이 중 general한 model로 둘다 RNN으로 이루어진 encoder와 decoder를 사용하는 방법이 있는데, encoder는 input seqeunce를 fixed length representation을 만들고, decoder는 output sequence를 만드는 역할을 합니다.
  • Vanila Sequence-to-Sequence architecture에서의 input sequence는 encoder에게만 한번 사용되고, output sequence는 encoder의 hidden state로부터 decoder가 만들어내게 됩니다. Bahdanau의 연구에서는 decoding step에서 input sequence를 더욱 잘 활용할 수있는 연구가 이루어졌고 또한, attention network가 도입되어 다양한 분야에서 활용되었습니다. 이 논문 또한 policy에서 attention을 사용하게 됩니다.
• Neural Combinatorial Optimization
  • Combinatorial optimization problems을 해결하기위해 다양한 연구들이 진행되었습니다. 이 때 NCO에서 이 문제의 dynamic input seqeunce length에 대해 Pointer Network를 적용하여 generalization을 보인 사례가 있습니다. 또한 graph embedding을 통한 연구가 이뤄진 사례도 있습니다.

The Model

• set of inputs \(X = \{x^i, i= 1, \cdots , M \}\)에 대해 decoding시점에서 input이 변할 수 있음을 허용합니다. 예를들면, VRP에서 vehicle이 nodes를 방문함에 따라 다른 nodes들의 요구량이 변한다든지, 새로운 nodes가 도착한다는 등의 input의 elements가 dynamic하게 변할 수 있습니다. 이를 표현하기 위해 각 input \(x^i\)에 대해 dynamic elements와 static input을 tuple로 나타냅니다. 이는 다음과 같습니다.

  \[\{ x^i_t = (s^i,d^i_t), t= 0,1, \cdots \}\]

  \(X_t\)는 고정된 시점 t에 대한 모든 input을 뜻합니다.

• input을 가리키는 pointer를 \(y_0\)로 표기하는데, decoding time t에서 \(y_{t+1}\)은 가능한 input \(X_t\)를 선택하고, 이는 또다시 decoder의 다음 input이 됩니다. 이는 어떤 종료조건이 만족되었을때 iteration이 멈추게 되는데, 이는 input sequence length랑 다를 수 있습니다. 이는 위에서 설명한 예로 다시 들면, depot을 다시 방문하거나 이미 들렀던 nodes를 또 방문할 수 있기 때문입니다. 결론적으로 이 \(Y_t = \{y_0,\cdots,y_t \}\)의 길이가 최소인 optimal policy에 대해 \(\pi^*\)로 나타낼 수 있고, 논문의 목표는 stochastic policy \(\pi\)를 \(\pi^*\)에 최대한 가깝게 만드는 것이 됩니다.

• input \(X_0\)에 대해 \(Y\)를 만드는 probability에 대해 나타내면 다음과 같이 나타낼 수 있습니다.

  \[P(Y \vert X_0) = \prod^T_{t=0}\pi(y_{t+1} \vert Y_t,X_t) \cdots (1)\]

  이 때, 우측 항의 pointer \(y_{t+1}\)는 dynamic element에 의해 영향을 받는 것을 고려하므로 conditional하게 나타냈습니다. \(X_{t+1}\)는 transition function \(f\)에 의해 다음과 같이 dynamic elements가 변함을 나타낼 수 있습니다.

  \[X_{t+1} = f(y_{t+1}, X_t) \cdots (2)\]

  결론적으로 policy는 \(\pi(\cdot \vert Y_t,X_t) = \mathrm{softmax}(g(h_t,X_t))\)로 나타낼 수 있는데, attention mechanism section에서 마저 설명하도록 하겠습니다.

• Remark 1 - static 환경과 dynamic 환경에 대해 둘다 학습 가능합니다. 애초에 agent는 transition function \(f\)를 approximation을 통해 추정하기 때문에 noise가 있더라도 충분히 학습가능함을 보입니다.

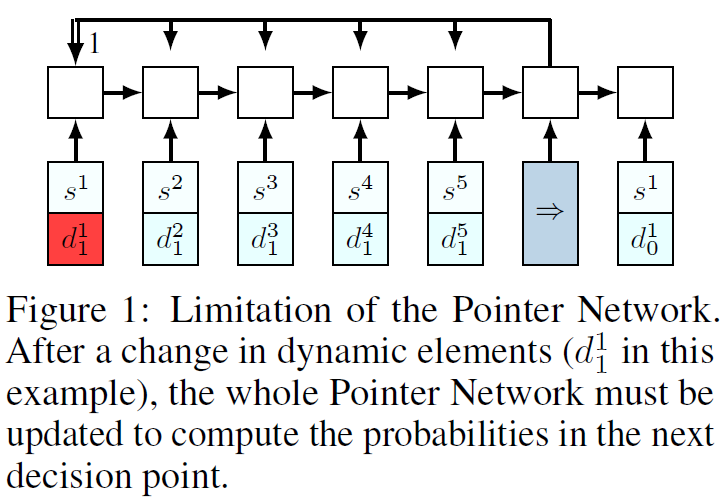
1. Limitations of Pointer Networks
   • NCO에서 사용된 framework는 VRP같은 더 복잡한 COP를 풀기엔 불충분합니다. 예를들어 보겠습니다.

   

   VRP에서의 예로 물류 배달을 할 때, \(s^1\)를 방문함으로써 dynamic information의 변화가 생겨 \(d^1_0 \neq d^1_1\)가 됩니다. 그러므로 다시 \(d^1_1\)에 대한 정보를 계산해야하고 gradient를 계산할 때에도 문제가 발생합니다. 이를 해결하기 위한 방법을 다음 section에서 제시합니다.

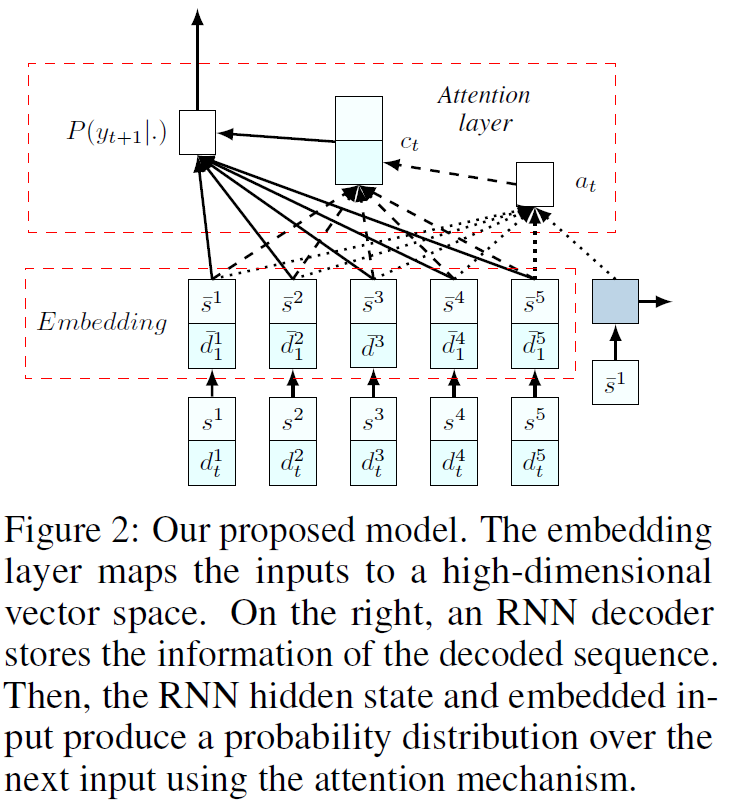
2. The Proposed Neural Network Model
   • 기존에 encoder에서 사용되었던 RNN의 불필요성을 주장합니다. RNN은 input의 sequential information을 얻기 위해 필요한데, input set에서는 그러한 정보가 전혀 존재하지 않습니다. 그렇기에 RNN을 없애고 embedding한 input을 그대로 사용하게 됩니다. 이는 다음 그림과 같습니다.

   

   이를 통해 model이 두가지 요소로 이루어져있음을 볼 수 있습니다.

   • 첫 째로 input을 d-dimensional vector space로 embedding하는 set이 있고, 이는 input의 종류에 따라 여러 방법이 존재합니다. 하지만 모든 input에 대해선 공유되는 형태를 띕니다.(RNN이 사라진 형태를 띕니다.)
   • 둘 째로, decoder는 RNN을 사용합니다. 이는 static element만이 input으로 들어가게 됩니다. 이 때, Auto-regressive하게 dynamic element와 static element 모두 다시 decoder로 들어갈 수 있지만, 성능향상은 이루어지지 않았습니다. 그렇기에 dynamic elements는 attention layer에서만 쓰이게 되는데, 이를 다음 section에서 설명하겠습니다.
3. Attention Mechanism
   • 각 input \(\bar{x}^i_t = (\bar{s}^i,\bar{d}^i_t)\)는 embedding된 상태의 static, dynamic element를 가진 하나의 input입니다. 이는 decoder의 RNN cell과 concatenate하여 context-based attention을 사용한 glimpse를 만들어 내는데, 이는 다음과 같습니다.
   \[a_t = a_t(\bar{x}_t,h_t) =\mathrm{softmax}(u_t),\ \ \mathrm{where}\ \ u^i_t = v^T_a\tanh{(W_a[\bar{x}^i_t;h_t])}\]

   이를 glimpsing하여 context vector \(c_t\)를 만듭니다.

   \[c_t = \sum^T_{i=1}a^i_t \bar{x}^i_t\]

   \(c_t\)를 이용하여 다시 \(\bar{x}\)에 대해 content-based attention을 하면, 다음 action에 대한 distribution을 얻을 수 있습니다. 이는 다음과 같습니다.

   \[\pi(\cdot \vert Y_t,X_t) = \mathrm{softmax}(\bar{u}_t) ,\ \ \mathrm{where} \ \ \bar{u}^i_t = v^T_c \tanh{W_c[\bar{x}^i_t;c_t]}\]

• Remark 2
  • 기존의 연구에서도 input sequence가 중요하지 않을 때 어떻게 network에게 전달해야하는지에 대해 이야기가 나왔고, pointer network가 적용될때도 해결되지 않았던 문제입니다. 하지만 이 model은 input order에 따른 영향을 받지 않습니다.

1. Training Method
   • Policy gradient를 통해 actor와 critic을 학습합니다. 본문에서 A2C와 A3C algorithm을 pseudo code로 나타내나 이전과 크게 다르지 않으므로 설명은 건너뛰겠습니다.

   

   

References

• Reinforcement Learning for Solving the Vehicle Routing Problem