Image Augmentation Is All You Need: Regularizing Deep Reinforcement Learning from Pixels 논문 리뷰 및 설명

Image Augmentation Is All You Need: Regularizing Deep Reinforcement Learning from Pixels

Abstract

• 이 논문은 data augmentation(perturbations)을 통해 value function을 regularization함으로써 auxiliary loss나 pretraining없이 vision-based benchmark인 DeepMind Control suite에서 SOTA를 보인 논문입니다.

Introduction

• RL agent의 convolutional encoder를 사용한 policy network는 environment와 제한된 interation, sample간의 상관관계, sparse reward signal문제로 인해 학습이 굉장히 어렵습니다. 이런 문제점들은 task를 optimize하기 위한 좋은 representation을 얻기 어렵게 합니다. 이는 AI 다양한 분야에서 일어나는 문제이기도 하며, 다양한 방법으로 접근한 연구들이 있습니다.
  1. training이전에 self-supervised learning을 통한 pretraining
  2. auxiliary loss를 추가하는 방법
  3. data augmentation을 이용하는 방법
• 1.은 이전에 포스팅했던 APS,VISR 같은 방법들이 있지만, 환경과의 interaction이 제한되었다는 점에서 한계가 명확하고, 2.는 다양한 연구들이 이뤄졌었지만, 근본적으로 직접 task에 연관된 objective를 optimize하지 않으므로, policy network가 적절한 representation을 유도한다는 보장이 없습니다. 논문은 3.의 방법을 사용합니다. 이는 vision이나 speech쪽에서 많이 적용되었으나, RL community에서는 주목하지 않았던 방법입니다. 이는 input을 perturb(section 4.1에서 설명합니다.)하여 같은 input에 대해 Q를 regularization하는 방식으로 추가적인 loss없이도 학습하는 방법을 제시합니다.
• 이 논문의 Contribution은 다음과 같습니다.
  1. Image augmentation을 통해 기본적인 RL algorithm의 변화없이 overfitting을 줄임을 보입니다.
  2. Value function을 regularization하는 두 가지 메커니즘을 소개합니다.
  3. Vanila SAC과 결합하여 모든 task에 hyper-parameter를 고정하고도 DeepMind Control suite에서 SOTA를 보입니다.
  4. Auxiliary losses나 model없이 pixel-based environment를 직접적으로 효과적이게 학습하기 위한 첫 접근입니다.
  5. 논문의 pytorch Implementation을 제공합니다.

Background

- Reinforcement Learning from Images

• 다음과 같은 infinte-horizon partially observable Markov decision process(POMDP)로 문제를 formulate합니다. POMDP는 다음과 같은 tuple \((\mathcal{O,A},p,r,\gamma)\)로 나타낼 수 있습니다.
• \(\mathcal{O}\) : high-dimensional observation space
• \(\mathcal{A}\) : action space
• \(p\) : transition dynamics \(p = Pr(o'_t \vert o_{\leq t},a_t)\)
• \(r\) : reward function \(r : \mathcal{O} \times \mathcal{A} → \mathbb{R}\), \(r_t = r(o_{\leq t},a_t)\)
• \(\gamma\) : discount factor \(\gamma \in [0,1)\)

이 때, 일반적으로 input을 연속적인 image를 stacking하여 POMDP를 MDP로 변환합니다. 그리하여, transition dynamics와 reward function을 다음과 같이 나타낼 수 있습니다. \(p = Pr(s'_t \vert s_t,a_t)\), \(r_t = r(s_t,a_t)\) 이를 이용해 cumulative discounted return \(\mathbb{E}_\pi[\sum^\infty_{t=1} \gamma^tr_t \vert a_t \sim \pi(\cdot \vert s_t), s'_t \sim p(\cdot \vert s_t,a_t),s_1 \sim p(\cdot)]\)를 maximize하는 policy \(\pi(a_t \vert s_t)\)를 찾게됩니다.

• Soft Actor-Critic
• Deep Q-learning

Sample Efficient Reinforcement Learning from Pixels

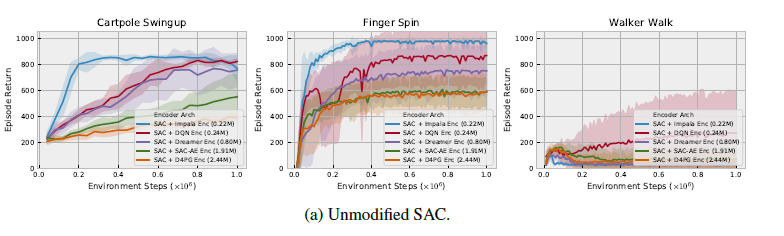
• 본 논문은 data-efficiency의 관점에서 집중하여 설명합니다.

  

  위의 그림을 보면, 다양한 algorithm으로 학습된 encoder에 대해 SAC에 붙였을 때, parameter가 증가할수록 성능이 떨어지는 overfitting이 일어난 것을 볼 수 있습니다.

1. Image Augmentation

• Image augmentation은 task label이 invarient한 경우에 자주 쓰이는 테크닉입니다. 예를들면 object detection의 경우, 이미지가 flip되거나 rotation되어도 label이 invarient합니다.

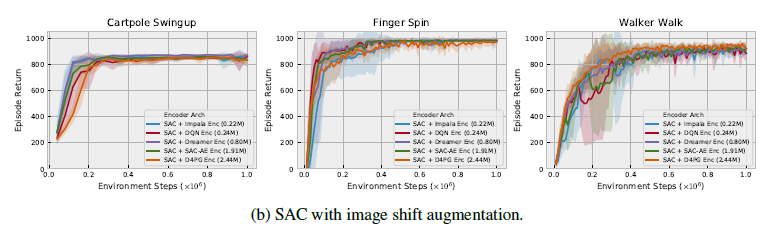
• 위의 그래프와 같은 상황에서 data sampling할 때마다 data augmentation을 한 후 SAC를 training하는 성능을 그래프로 나타내면 다음과 같습니다.

  

  이는 data augmentation을 적용했을 때 각 encoder에 따라 성능 차이가 거의 일어나지 않음을 볼 수 있고, overfitting을 막는데 이 방법이 유효했음을 보입니다.

• 다양한 image transformation(data augment를위한)중에서도 random shifts가 적당했음을 appendix에서 실험적으로 보입니다. 이는 DeepMind Control suite에서 주어지는 image가 84 X 84이므로 이에 맞춰서 설명하면, 학습을 위해 이미지 sampling시 boundary pixel을 반복하여 4 pixel padding한 후 random하게 다시 84 X 84로 crop하여 진행합니다. 이는 image가 \(\pm 4\) pixel random하게 움직이는 것과 같습니다.(이를 perturb라고 표현합니다.)

2. Optimality Invariant Image Transformation

• 지금까지 본 image augmentation를 통해 학습시키는 방법도 충분히 효과적이지만, 또 이를 통해서 value function을 regularizing할 수 있는 방법이 있습니다. 이를 위해 optimality invariant state transformation \(f\)를 정의합니다. 이는 이름 그대로 이를 통해 state를 transformation하더라도, optimality(Q)에 대해선 invariant하다는 의미가 있습니다. \(f : \mathcal{S \times T → S}\)

  \[Q(s,a) = Q(f(s,\nu),a) \ \mathrm{for\ all }\ s \in \mathcal{S}, a \in \mathcal{A}\ \mathrm{and} \ \nu \in \mathcal{T}\]

  transformation \(f\)는 pararmeter \(\nu\)를 가지는데, 이는 각 sample에 대해 다른 transformation을 해주기 위해 사용합니다.

  transformation \(f\)는 각 state에 대해 같은 Q value를 가지는 다양한 states를 만드므로, Q-function estimation의 variance를 낮춰줄 수 있습니다. 그리하여 Q value를 추정할 때 하나의 sample \(s^* \sim \mu(\cdot), a^* \sim \pi(\cdot \vert s^*)\)이 아닌 다음과 같은 임의의 state distribution \(\mu(\cdot)\)과 policy \(\pi\)에 의한 expectation으로 나타낼 수 있습니다.

  \[\mathbb{E}_{s \sim \mu(\cdot), a \sim\pi(\cdot \vert s )}[Q(s,a)] \approx Q(s^*,a^*)\]

  그리고, 이를 K 개의 random transformation을 거친 samples을 통해 근사할 수 있습니다.

  \[\mathbb{E}_{s \sim \mu(\cdot), a \sim\pi(\cdot \vert s )}[Q(s,a)] \approx \frac{1}{K}\sum^K_{k=1}Q(f(s^*,\nu_k),a_k) \ \ \mathrm{where} \ \ \nu_k \in \mathcal{T} \ \ \mathrm{and} \ a_k \sim \pi(\cdot \vert f(s^*,\nu_k))\]

  이 때, 두 개의 Q function을 regularize하는 방법을 제시하는데 첫째로, target value를 구할 때 data augmentation을 사용합니다.

  \[y_i = r_i + \gamma \frac{1}{K}\sum^K_{k=1}Q_\theta(f(s'_i,\nu'_{i,k}),a'_{i,k})\ \mathrm{where}\ a'_{i,k} \sim \pi(\cdot \vert f(s'_i,\nu'_{i,k})) \cdots(1)\]

  \(s'\)와 \(\nu'\)는 next state와 next state에 대응하는 transformation의 parameter입니다. 이를 통해 기존의 Q-learning와 동일하게 Q를 업데이트하면됩니다.

  \[\theta ← \theta - \lambda_\theta \nabla_\theta\frac{1}{N}\sum^N_{i=1}(Q_\theta(f(s_i,\nu_i),a_i)-y_i)^2 \cdots (2)\]

  여기에서 추가로 (1)과 동일하게 Q value를 estimation할 때도, 동일한 image에 대해 다음과 같이 transformation을 이용할 수 있습니다.

  \[\theta ← \theta - \lambda_\theta \nabla_\theta\frac{1}{NM}\sum^{N,M}_{i=1,m=1}(Q_\theta(f(s_i,\nu_{i,m}),a_i)-y_i)^2 \cdots (3)\]

Our approach : Data-regularized Q(DrQ)

• DrQ는 다음과 같은 세 가지의 regularization mechanisms을 가지고 있습니다.
  1. input image를 transformation하는 것
  2. Q target을 K개의 image transformations에 대해 평균내는 것
  3. Q function을 데이터 하나에 대해 M개의 transformations을 만들어 평균내는 것

  마지막으록 algorithm을 보겠습니다.

  

  위에서 설명한 내용 그대로이므로 설명을 더 붙이진 않겠습니다. 마지막으로, K=1,M=1일 때, DrQ는 image transformation만 하여 학습하는 것과 동일한데, 이는 RAD와 동일한 방법입니다.

References

• Image Augmentation Is All You Need : Regularizing Deep Reinforcement Learning from Pixels