Pay Attention to MLPs
Abstract
Transformer는 다양한 deep learning 분야에서 큰 영향을 끼쳤습니다. 여기서 논문은 inductive bias relaxation을 시도한 gMLP(MLPs with gating)을 제시합니다.
Introduction
Transformer는 NLP와 CV 다양한 분야에서 돌파구를 만들었습니다. 이러한 성공들은 NLP에서 주로 사용되던 recurrent layer들을 대부분 대체하였고, ConvNets에도 뒤지지않는 성능들을 보였습니다.
이 Transformer architecture의 두 가지 concepts을 얘기하자면 다음과 같습니다.
- recurrent layer없이 각 token을 병렬적으로 계산가능한 점
- multi-head self-attention block을 통해 각 token간의 spatial information을 통합했다는 점
- attention mechanism과 함께 각 token에 inner product하여 각 token별로 곱해주는 방식에 대해 dynamically parameterized했다라는 표현을 합니다.
- 이는 positional encoding과 함께 사용된 inductive bias임을 알 수 있습니다.
- 반대로 MLP는 각 자리에 맞는 weights를 그냥 계산하는 방식이므로 이와 반대로 static parameterized라고 표현합니다.
- attention mechanism과 함께 각 token에 inner product하여 각 token별로 곱해주는 방식에 대해 dynamically parameterized했다라는 표현을 합니다.
- gMLP를 masked language modeling(MLM)에서도 실험. perplexity는 self-attention의 존재와 무관하게 model의 capacity와 주로 correlated되었음. pretraining혹은 finetuning에서도 gMLP는 Transformer과 비슷한 속도로 개선됨을 보임.
Model
gMLP는 L개 block을 사용한 structure를 가짐. block하나를 표현하면 다음과 같습니다.
- \(X \in \mathbb{R}^{n \times d}\), \(U \in \mathbb{R}^{d \times h}\)
- \(Z=\sigma (XU)\), \(\tilde{Z} = s(Z)\), \(Y=\tilde{Z}V\)
- activation function GeLU
- h는 hidden으로 U와 V는 transpose한 dimension을 가질수도, 이후에 설명할 두개로 쪼개질 경우 다른 dimension을 가질 수도 있습니다.
- \(s(\cdot)\)는 아래서설명하도록 하고, s가 identity mapping이라면 각 token은 아무 교류없이 넘어가게됩니다. 그렇기때문에 어떻게 좋은 s를 찾느냐가 관건이 됩니다.
Spatial Gating Unit
- \(W \in \mathbb{R}^{n\times n}\), \(f_{W,b}(Z) = WZ+b\), \(s(Z) = z \cdot f_{W,b}(Z)\)
- WZ가 XU와 순서가 바뀜에 유의해야합니다. 이는 각 x의 i번째 elements의 weight sum을 의미합니다.
- \(W\)를 zero matrix에, b를 1 vector로 초기화하는 것이 적당한 전략으로 보이고 논문도 이를 적용하였습니다.
- 이때, 위에서 잠깐 언급했지만 \(Z\)를 \((Z_1,Z_2)\)로 나누어 \(s(Z)=Z_1 \cdot f_{W,b}(Z_2)\)로 계산하였을 때 더 좋은 성능을 보였고, 이후에 SGU의 다양한 변형들을 보였습니다.
- time complexity
- gNLP는 n^2 e/2
- self attention은 2n^2 d 로 d와 n이 적당히 같다 근사하여 나온 값입니다.
Image Classification
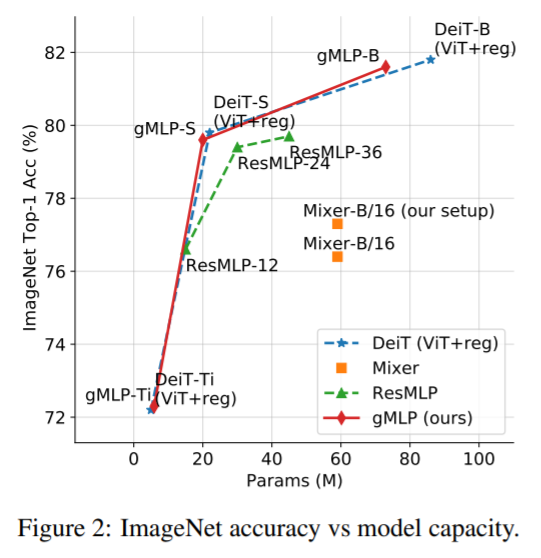
ImageNet dataset에 대한 classification task 실험을 진행합니다. vanila tansformer, MLP-like 모델, ViT에 대한 비교가 있습니다. 이때 다른 transformer에서처럼 overfitting발생하기 때문에, DeiT와 같은 regularization을 적용합니다.
이는 적당히 regularization만 된다면 self attention보다 network의 capacity에 달려있다는 증거가 됩니다.
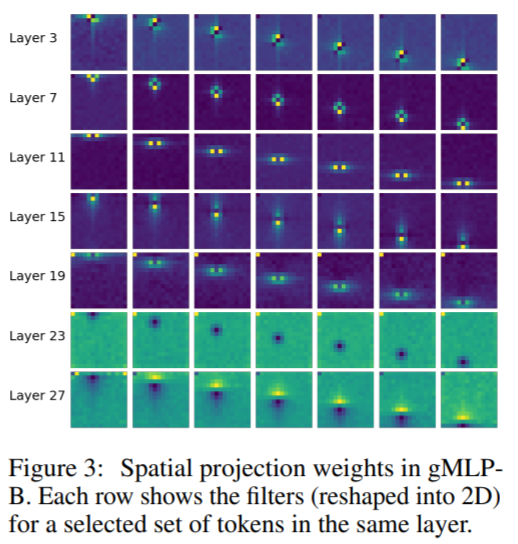
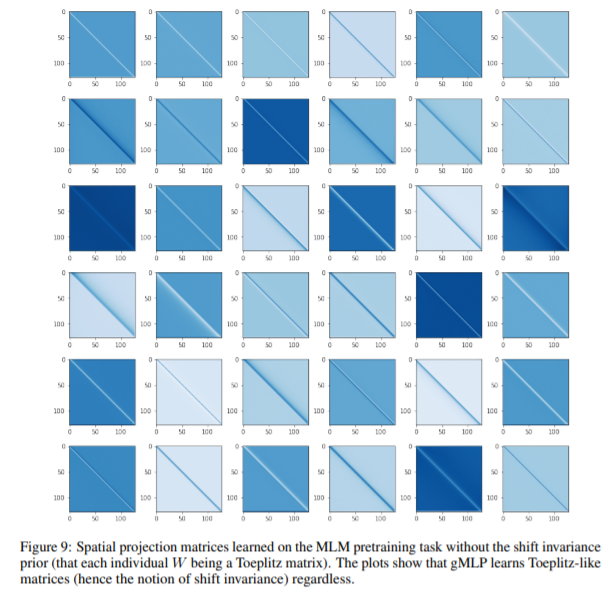
gMLP-B에서 적당한 tokens에 대한 spatial projection matrices를 보입니다. spatial weights를 통해 locality와 spatial invariance가 학습된 것을 볼 수 있습니다.
Masked Language Modeling with Bert
BERT와 양식 같게 실험을 진행합니다. 이전에 언급했지만, positional encoding가 없고,
Ablation : The Importance of Gating in gMLP for BERT’s Pretraining
BERT에서 다양한 ablation studies를 진행한 결과입니다.
중간 token에 대해 각 token이 얼마나 associated 되어있는지 spatial filter를 출력하면 다음과 같습니다.
Case Study : The Behavior of gMLP as Model Size Increases
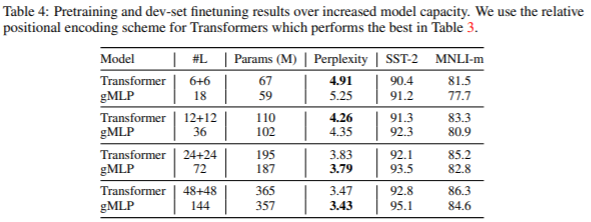
중간 n+n은 self-attention과 feed forward network를 따로 나타낸 것입니다.
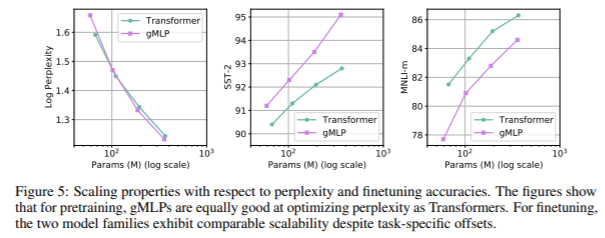
모델이 커진다면 충분히 gMLP가 Transformer가 encoding했던 spatial information에 대해 충분히 표현가능함을 성능적으로 보입니다.
외에도 perplexity가 같다해도 finetuning에는 inductive bias같은 요소들이 또 영향을 미침을 알 수 있는데, 다만 그래프를보면 capacity에 따른 성능의 기울기가 보이므로 적당히 극복가능한 요소라고 판단하고 있습니다.
Ablation : The Usefulness of tiny Attention in BERT’s Finetuning
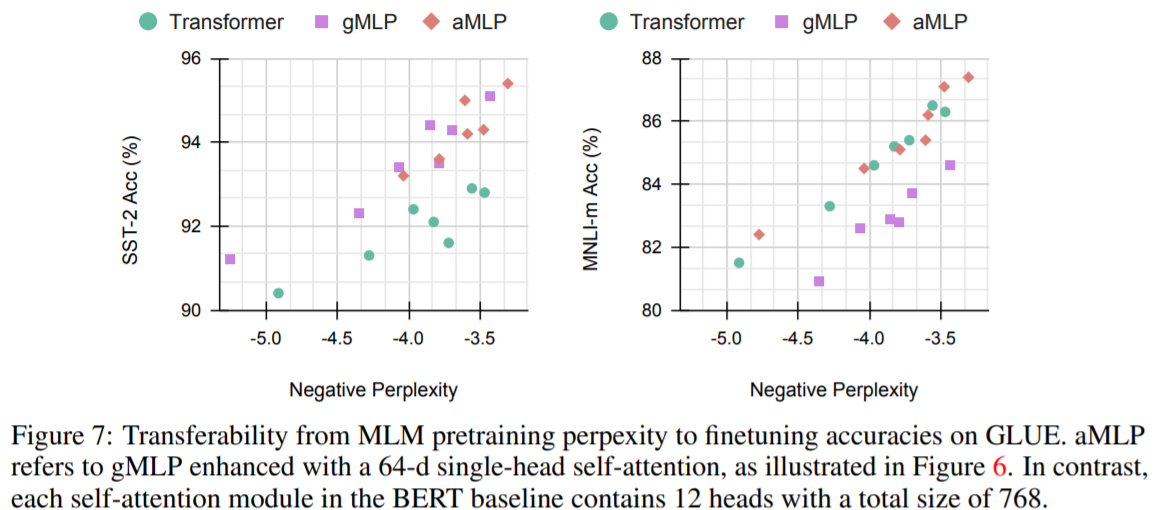
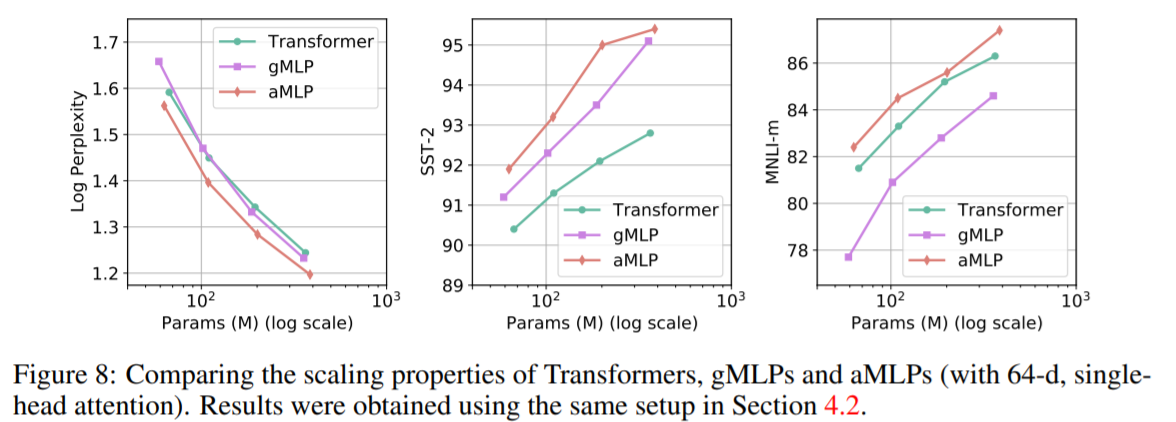
tiny attention을 추가하는 것이 Fig5에서 MNLI-m에서 Transformer보다 안좋았던 성능에 대해 해결해줌을 보입니다. 이를 통해 Positional encoding없이 spatial information이 gMLP block에 잘 encoding되었고, 성능이 좋아진 이유는 3rd-order interaction이 일어나며 성능향상이 일어난것 으로 추정할 수 있습니다.
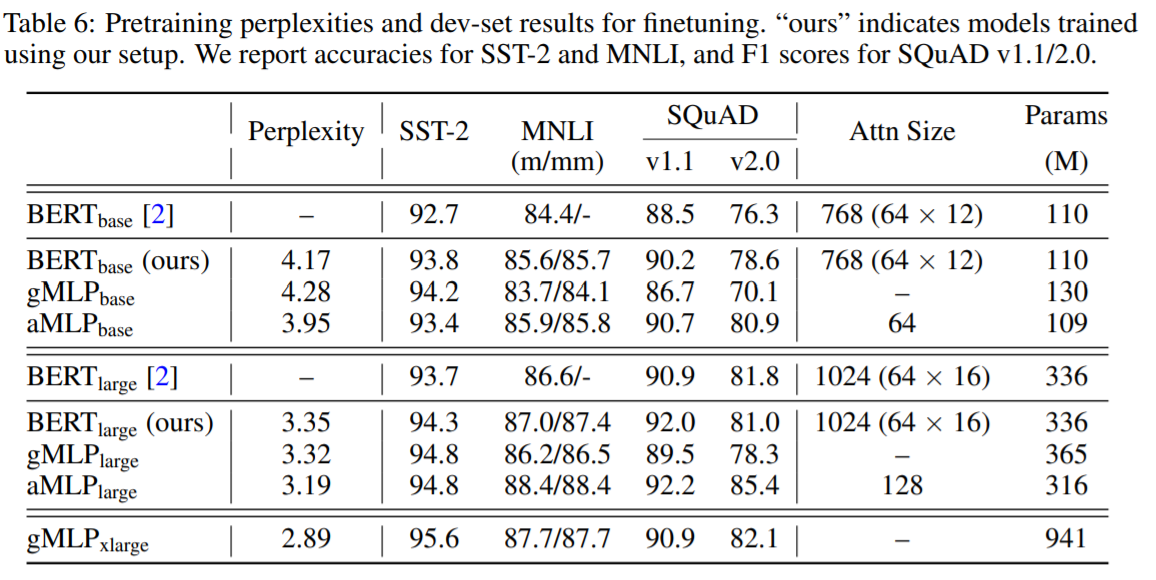
Main Results for MLM in the BERT Setup
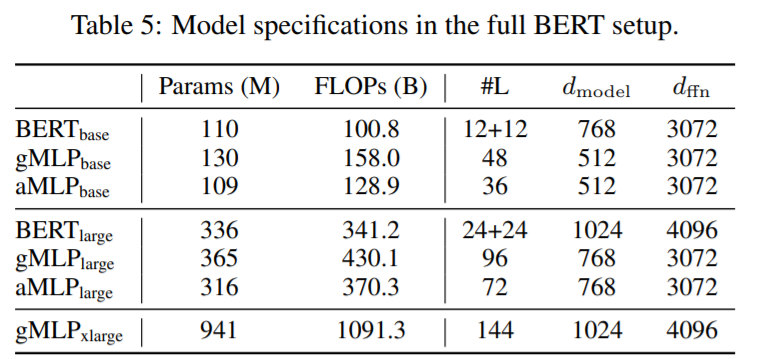
table 5와 같은 setup으로 table 6의 성능을 보이는 것으로 논문을 마무리합니다.
References
- Liu, H., Dai, Z., So, D. R., & Le, Q. V. (2021). Pay Attention to MLPs. arXiv preprint arXiv:2105.08050.
- Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., … & Polosukhin, I. (2017). Attention is all you need. In Advances in neural information processing systems (pp. 5998-6008).
- Mitchell, T. M. (1980). The need for biases in learning generalizations (pp. 184-191). Piscataway, NJ, USA: Department of Computer Science, Laboratory for Computer Science Research, Rutgers Univ.
- Kim, H. (n.d.). [NLP 논문 구현] pytorch로 구현하는 Transformer (Attention is All You Need). Hansu Kim’s Blog. https://cpm0722.github.io/pytorch-implementation/transformer
- Kazemnejad, A. (n.d.). Transformer Architecture: The Positional Encoding - Amirhossein Kazemnejad’s Blog. https://kazemnejad.com/blog/transformer_architecture_positional_encoding/
- Srivastava, R. K., Greff, K., & Schmidhuber, J. (2015). Highway networks. arXiv preprint arXiv:1505.00387.
- Hu, J., Shen, L., & Sun, G. (2018). Squeeze-and-excitation networks. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 7132-7141).