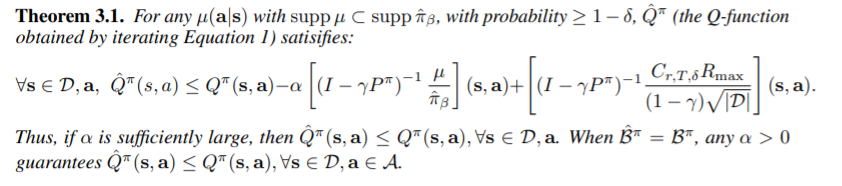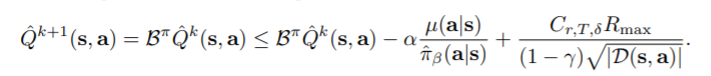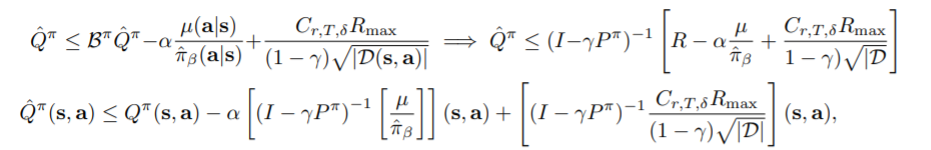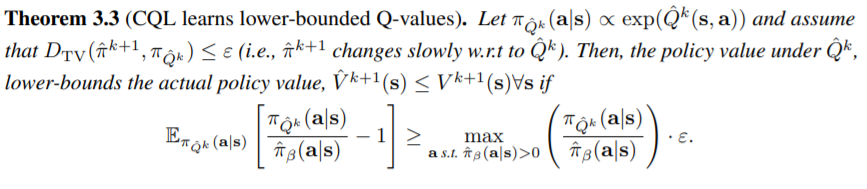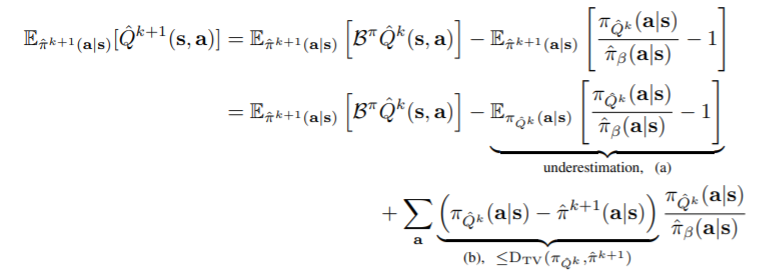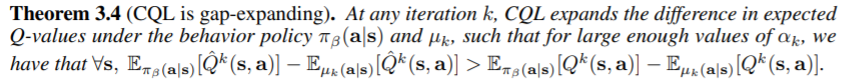Conservative Q-Learning for Offline Reinforcement Learning 논문 리뷰 및 설명

Conservative Q-Learning for Offline Reinforcement Learning

Abstract

• Setting
  • 실제 아주 큰 환경에서 이전에 많이 모은 데이터 셋을 활용하여 RL을 할 때, 어떤 방식으로 접근하는 것이 좋을까?
• Problems
  • Overestimation
    • off-policy method를 사용했을 때, 항상 target과 behavior policy에 대한 distribution에 대한 염두를 해야합니다. 하지만 offline RL같이 완전히 고정된 데이터셋에서 policy를 optimize해야하는 문제는 “updated policy에 대한 trajectories를 받아올 수 없다”를 가정하므로 distribution shift가 심화됩니다.
• Solutions
  • 이 논문에서는 Conservative Q Learning을 통해 이를 해결합니다. 이는 이름 그대로 conservative Q function을 배움으로써 해결하는데, 이 Q function은 실제 Q value의 하한을 가집니다.

Introduction

• Offline Learning은 데이터를 얻기 어려운 상황 혹은 데이터가 너무 느리게 축적되는 경우 생각해 볼 수 있는 방법입니다.
• Offline Learning의 표현 범위가 너무 넓어(데이터를 축적하여 policy를 update하면 offline learning이라 하므로(ex MC learning)) 위에서 말한 상황 가정에 대해 batch RL이라고 표현해줄 수도있습니다.
• 실제로 전형적인 value-based off-policy algorithms은 이러한 상황에서 제대로 학습되지 않는 모습들을 보입니다. 좀 더 깊은 이유에 대해선 deadly triad관련해서 블로그 내의 글을 확인해보시면 도움이됩니다.
• 본 논문에서는 점별로(각 true state value와 estimated state value별로) lower bound를 만들어주기 위해 현재 policy에 따른 distribution를 q value에 대한 minimize term과 데이터를 수집할때의 policy q value에 대한 maximize term을 두는데 section 3에서 자세히 설명하도록 하겠습니다.

Preliminaries

• 일반적인 RL problem setting과 같이 expected cumulative discounted reward Markov decision process \((\mathcal{S},\mathcal{A},T,r,\gamma)\)를 가정합니다. Dataset \(\mathcal{D}\)를 얻은 behavior policy \(\pi_\beta(\boldsymbol{a}\vert \boldsymbol{s})\)와 empirical behavior policy \(\hat{\pi}_\beta(\boldsymbol{a}\vert \boldsymbol{s}) :=\frac{\sum_{\boldsymbol{s},\boldsymbol{a}\in\mathcal{D}}\boldsymbol{1}[\boldsymbol{s}=\boldsymbol{s},\boldsymbol{a}=\boldsymbol{a}]}{\sum_{\boldsymbol{s}\in\mathcal{D}}\boldsymbol{1}[\boldsymbol{s}=\boldsymbol{s}]}\)에 대한 설명이 있습니다. 이런 hat 기호는 empirical하게 얻은 값 혹은 이후에 나올 empirical bellman operator를 사용해 얻은 값을 표기하기 위해 사용됩니다.

• 설명에 앞서 Actor-Critic method에서 Policy evaluation과 Policy Improvement를 진행할 때, Dataset \(\mathcal{D}\)에서는 multi-step learning이 어려움이 자명합니다. 그렇기에 empirical Bellman operator를 도입하여 single step update만을 진행하는데, \(\pi_\beta\)에 의해 수집된 dataset에 대해 \(\hat{\mathcal{B}}^\pi\)로 표기하고 연산은 다음과 같습니다. hat이 달린 표기는 empirical bellman operator에 의한 값임을 나타냅니다.

  \[\hat{Q}^{k+1} ← \mathrm{argmin}_Q\mathbb{E}_{\boldsymbol{s,a,s'}\sim \mathcal{D}}[((r(\boldsymbol{s},\boldsymbol{a})+\gamma \mathbb{E}_{\boldsymbol{a}'\sim\pi^k(\boldsymbol{a'} \vert \boldsymbol{s'})}[\hat{Q}^k(\boldsymbol{s}',\boldsymbol{a}')])-Q(\boldsymbol{s},\boldsymbol{a}))^2] \cdots\mathrm{policy\ evaluation}\] \[\hat{\pi}^{k+1}← \mathrm{argmax}_{\pi}\mathbb{E}_{\boldsymbol{s}\sim\mathcal{D},\boldsymbol{a}\sim\pi^k(\boldsymbol{a}\vert \boldsymbol{s})}[\hat{Q}^{k+1}(\boldsymbol{s},\boldsymbol{a})] \cdots \mathrm{policy\ improvement}\]

  이러한 empirical bellman operator의 연산은 action distribution shift 현상을 겪습니다. 이는 policy evaluation과정의 target value는 학습중인 policy \(\pi^k\)에 의해 값이 구해지지만, q function은 결국 Dataset의 분포에서 나온 action으로만 학습함으로 인해 생기는 현상입니다. 이런 현상은 out-of-distribution(OOD) action에게 높은 Q value를 할당하는 경향을 만들게 됩니다.(OOD인 action은 Dataset에 없으므로 그 overestimation을 교정하기 어려움) 결국 이 empirical bellman operator를 통해 알 수 있는 점은 OOD states에 대한 문제는 policy가 겪을 수 있는 문제임을 policy improvement step 수식에서 알 수 있습니다.

The Conservative Q-Learning(CQL) Framework

1. Conservative Off-Policy Evaluation

   • 가장 큰 문제로 나타나는 overestimation는 unseen state에 대한 q-value의 문제가 아닌 unseen action에 대한 문제이므로, 본 논문은 action에 대한 특정 marginal distribution \(\mu\)를 penalty term으로 두어 이를 해결하려 합니다. 이를 표현하면 다음과 같습니다.

     \[\hat{Q}^{k+1} ← \mathrm{argmin}_{Q} \alpha \mathbb{E}_{\boldsymbol{s}\sim \mathcal{D},\boldsymbol{a}\sim\mu(\boldsymbol{a}\vert\boldsymbol{s})}[Q(\boldsymbol{s},\boldsymbol{a})]+\frac{1}{2}\mathbb{E}_{\boldsymbol{s},\boldsymbol{a}\sim \mathcal{D}}[(Q(\boldsymbol{s},\boldsymbol{a})-\hat{\mathcal{B}}^\pi\hat{Q}(\boldsymbol{s},\boldsymbol{a})^2] \cdots(1)\]

     이렇게 무한히 업데이트하면 결국 \(Q^\pi\)의 point-wise lower bound가 되는데, 이를 증명해보겠습니다.

     

     다음을 증명하겠습니다. 이는 다음과 같이 시작합니다. (1)에서 importance sampling을 해준뒤 Q의 derivative가 0이되는 Q를 찾으면 이는 다음과 같습니다.

     \[\forall \boldsymbol{s},\boldsymbol{a} \in \mathcal{D},k\in \mathbb{N},\ \hat{Q}^{k+1}(\boldsymbol{s},\boldsymbol{a})= \hat{\mathcal{B}}^\pi\hat{Q}^k(\boldsymbol{s},\boldsymbol{a}) - \alpha \frac{\mu(\boldsymbol{a}\vert\boldsymbol{s})}{\hat{\pi}_\beta(\boldsymbol{a}\vert\boldsymbol{s})}\]

     이는 RHS의 \(\alpha, \mu, \hat{\pi}_\beta\)가 각각 양수로 가정, \(\mu\)의 support set은 \(\hat{\pi}_\beta\)에 포함되므로 두번째 term이 모두 양수의 마이너스를 한 것이 되어 항상 \(\hat{Q}^{k+1} \leq \hat{\mathcal{B}}^\pi\hat{Q}^k\)임을 알 수 있습니다. 그리고 Appendix D.3에 좀더 자세히 나와있지만, reward function과 transition matrix가 적당한 \(\delta\)를 잡아 \(1-\delta\)보다 높은 확률로 bound되어있다면 empirical Backup operator도 bounded이다라는 점을 이용해 다음과 같이 나타낼 수 있습니다. \(C_{r,T,\delta}\)는 세가지 변수에 의존한 상수입니다.(reward의 최댓값이 \(R_{\max}\)이므로, \(Q\)를 \(\frac{R_{\max}}{1-\gamma}\) 보다 작게 bound시킬 수 있습니다.)

     \[\forall Q,\boldsymbol{s},\boldsymbol{a} \in \mathcal{D}, \vert \hat{\mathcal{B}}^\pi Q(\boldsymbol{s},\boldsymbol{a}) -\mathcal{B}^\pi Q(\boldsymbol{s},\boldsymbol{a}) \vert \leq \frac{C_{r,T,\delta}R_{\max}}{(1-\gamma)\sqrt{\vert \mathcal{D}(\boldsymbol{s},\boldsymbol{a})\vert}}\]

     이는 다음과 같이 쓸 수 있습니다.

     

     이후는 Bellman operator의 성질을 이용하여 trivial하게 얻을 수 있습니다.

     

     alpha의 범위에 대해 trivial하므로 다루지않겠습니다. 또 이후의 증명에서는 empirical bellman update를 통해 나타난 sampling error는 마지막에 붙이는 형식으로 증명하므로 유의해두면 좋습니다.

   • \(\hat{Q}\)을 좀 더 \(V^\pi(\boldsymbol{s})\)에 가깝도록 lower bound를 구하기 위해 다음과 같이 \(Q\)를 maximize하는 term을 넣을 수 있습니다. 다만 이를 통해 다시 point-wise lower bound의 성질은 잃지만 \(\mu = \pi\)일 때, empirical value function이 state에 대해 lower bound가 다시 됨을 Theorem 3.2에서 볼 수 있습니다. 왜 point-wise lower bound를 얻고싶어했으면서 이러한 성질을 잃으면서까지 수식을 전개해가는지는 저자의 알고리즘이므로 알 수 없습니다.

     \[\hat{Q}^{k+1} ← \mathrm{argmin}_{Q} \underline{\alpha \cdot (\mathbb{E}_{\boldsymbol{s}\sim \mathcal{D}, \boldsymbol{a} \sim \mu(\boldsymbol{a} \vert \boldsymbol{s})}[Q(\boldsymbol{s},\boldsymbol{a})]-\mathbb{E}_{\boldsymbol{s}\sim \mathcal{D},\boldsymbol{a}\sim\hat{\pi}_\beta(\boldsymbol{a}\vert\boldsymbol{s})}[Q(\boldsymbol{s},\boldsymbol{a})])} +\frac{1}{2}\mathbb{E}_{\boldsymbol{s},\boldsymbol{a},\boldsymbol{s'}\sim\mathcal{D}}[(Q(\boldsymbol{s},\boldsymbol{a})-\hat{\mathcal{B}}^\pi\hat{Q}^k(\boldsymbol{s},\boldsymbol{a})^2] \cdots(2)\]

     (1)에서 부터 새로 생긴 term에 대해 꼭 behavior policy \(\hat{\pi}_\beta\)에 대해서 update를 해야하냐했을 때는 yes입니다. Appendix D.2에서 (2)의 underline term을 concave-convex maxmin optimization problem으로 치환해서 푸는데 Lagrangian method를 안다면 막히는 부분없이 읽을 수 있습니다. (22)의 \(\pi_\beta\)의 부호가 거꾸로 됐다는 점도 알 수 있습니다. 그러나 결과에는 지장이 없습니다. (policy가 full support라는점으로 \(\zeta(\boldsymbol{s},\boldsymbol{a})\)가 항상 0이라는점, \(\eta\)가 normalized lagrange dual variable 이라는 점만 유의하면 됩니다.) 결과적으로 \(\hat{\pi}_\beta\)가 아닌 다른 분포에 대해선 하한을 보장할 수 없게 된다는 것이 주요 내용입니다. 종합하여 우리는 value function에 대한 lower bound를 Theorem 3.1처럼 유도해낼 수 있습니다.

     

     이에 대한 증명도 Appendix C에 자세히 나와있습니다. 크게 어렵지 않아 생략하겠습니다. 이 때, \(\mu = \pi\)로 치환하는데, 이도 lower bound를 보장하기 위함이고 쉽게 증명되어 있습니다. 이를 통해 우리는 \(\hat{V}^{k+1}(\boldsymbol{s})\leq \mathcal{B}^{\pi}\hat{V}^k\)임을 알 수 있습니다.

2. Conservative Q-Learning for Offline RL
   • 이번 챕터는 어떤식으로 policy를 update해야할지에 얘기합니다. 현재 q value를 update할 때 Theorem 3.2에서 얘기한 것 처럼 \(\mu = \pi\)여야하므로, 계속 Q의 expectation을 policy에 대해 구해야합니다. 본 논문은 이 과정을 inner maximization을 넣어 policy를 구하는 방식을 취합니다. 이 때, policy의 generalization을 위해 regularizer를 추가합니다.
   \[\min_Q\max_\mu\alpha(\mathbb{E}_{\boldsymbol{s}\sim\mathcal{D},\boldsymbol{a}\sim \mu(\boldsymbol{a}\vert\boldsymbol{s})}[Q(\boldsymbol{s},\boldsymbol{a})] - \mathbb{E}_{\boldsymbol{s}\sim\mathcal{D},\boldsymbol{a}\sim\hat{\pi}_\beta(\boldsymbol{a}\vert\boldsymbol{s})}[Q(\boldsymbol{s},\boldsymbol{a})]) + \frac{1}{2}\mathbb{E}_{\boldsymbol{s},\boldsymbol{a},\boldsymbol{s'}\sim \mathcal{D}}[(Q(\boldsymbol{s},\boldsymbol{a}- \hat{\mathcal{B}}^{\pi_k}\hat{Q}^k(\boldsymbol{s},\boldsymbol{a}))]+\mathcal{R}(\mu) \cdots (3)(\mathrm{CQL}(\mathcal{R}))\]
   • Variants of CQL

     • regularizer를 어떤걸 쓰냐 생각해볼 수 있지만 논문에서도 역시 가장 만만한 KL-divergence를 사용했습니다. 이 때, 기준이 되는 distribution이 필요하고 이를 \(\rho(\boldsymbol{a}\vert\boldsymbol{s})\)로 표현합니다. 본문에서는 uniform distribution 혹은 previous policy를 제시하였습니다. 이 때, \(\mu(\boldsymbol{a}\vert\boldsymbol{s})\)의 form에 대해 \(\mu(\boldsymbol{a}\vert\boldsymbol{s}) \propto \rho(\boldsymbol{a}\vert\boldsymbol{s}) \cdot \exp(Q(\boldsymbol{a}\vert\boldsymbol{s}))\)로 유도 가능하고 이는 Appendix A에 나타나있습니다. 이를 유도하는 방식 또한 Appendix D.2에서의 테크닉과 동일하게 lagrange method를 사용하면 됩니다. 다만 CQL(\(\mathcal{H}\))는 본문에서는 uniform distribution와의 kl divergence를 구하는 식으로 유도된다했으나 uniform distribution은 상수처럼 취급되어서 entropy랑 같은 역할을 하는건지 Appendix에서는 entropy를 더해주어 soft q learning과 같은 q 식을 만들어 냅니다.

       

       아래와 같이 CQL(\(\rho\))도 유도됩니다.(kl divergence를 minimize)

       

       이러한 테크닉은 high-dimensional action space에서 좀더 좋은 성능을 냅니다.

   • 다음으로는, policy가 update될때 실제로 conservative한지에 대해 증명합니다.

     

     이는 k-step의 policy가 다음과 같을 때, \(\hat{V}^{k+1}(\boldsymbol{s}) \leq V^{k+1}(\boldsymbol{s}) ,\forall \boldsymbol{s}\)임을 보입니다.

     

     그냥 \(\hat{V}^{k+1}\)의 수식을 풀어 underestimation부분이 total variance보다 작을 때, 즉 step마다 policy의 update가 작을 때에 대해 성립함을 말하고 있습니다.

   • Theorem 3.4는 사실 너무 직관적으로는 너무 당연합니다. empirical bellman update를 할때 (2)에서 보다시피 \(\pi_\beta(\boldsymbol{a} \vert \boldsymbol{s})\)에 대한 maximize term이 있기 때문입니다. 증명과정도 어렵지 않습니다. \((\pi_\beta(\boldsymbol{a}\vert\boldsymbol{s}) -\mu_k(\boldsymbol{a}\vert \boldsymbol{s}))^T\mathcal{B}^{\pi^k}Q^k(\boldsymbol{s},\cdot)\)은 \(D_{\mathrm{TV}}(\pi_\beta,\mu_k) \cdot \frac{R_{\max}}{1-\gamma}\)에 bound됐다는 점만 유의하면 쉽게넘어가는데, 증명과정중에도 나와있는내용이라 딱히 덧붙일 말이 없습니다.. 다만 이런 특성으로 인해 dataset distribution에 대한 q value가 높아서 policy가 dataset distribution에 크게 벗어나지 않게된다는 점만 기억하면 좋을 것 같습니다.

     

3. Safe Policy Improvement Guarantees

   CQL에서 Safe policy improvement with baseline bootstrapping의 Theorem을 따라 safe policy improvement를 하는 과정을 보이나 비중상 크게 중요하지 않아서 넘어갑니다.(논문의 practical algorithm 소개에서도 쓰이진 않습니다.) Appendix D.4에 자세히 나와있습니다. 결국 dataset크기가 충분히 크면 behavior policy의 improvement를 이끌 수 있음을 보입니다.

Practical Algorithm and Implementation Details

• CQL은 actor-critic 형태로도, Q-learning형태로도 적용이 가능함을 볼 수 있는데, actor-critic algorithm은 SAC같은 algorithm을 base로, Q-learning은 DQN같은 algorithm을 base로 적용합니다. 이 때, line 3에서 (3)의 수식을 통해 loss를 구하는데, 이때 쓰이는 bellman equation를 서로 다르게 적용하는것에 유의해야 합니다(당연하지만). 그리고 이전 알고리즘들과 다르게 따로 policy에 대한 constraint를 주지않았는데 이는, 이미 Q-function의 update에 대한 constraint가 있기 때문에 큰 신경을 써주지않아도 됩니다. 마지막으로 \(\alpha\)를 어떤식으로 값을 부여했느냐에 대한 얘기가 있는데, continuous control에서는 lagrangian dual gradient descent를 통해 조정했고, discrete control에서는 fix한채로 사용했습니다. 디테일한 내용은 Appendix F에 적혀져있습니다.

References

• Conservative Q-Learning for Offline Reinforcement Learning