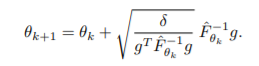Natural Policy Gradient 논문 리뷰

##1. Description

• 이전의 policy gradient에서의 policy network update는 1차 미분만을 사용해서 진행했는데, 이는 non-covariant하다. covariant하다는 말은 어떤 의미일까?
  • 리만 공간(Riemannian space)에서의 두 점의 거리는 두 점이 놓여있는 공간에 의해 결정되는데, 이는 어떤 metric tensor를 이용해 표현할 수 있다. 이는 거리가 metric tensor와 covariant하다고 할 수 있다. 보통의 Neural Network를 사용한 parameter space는 보통 리만 공간에 mapping된다. 왜 리만 공간인가를 생각해보면, input으로 들어온 data의 차원을 비선형함수와 구조로 parameter space를 변형시키기 때문이다. 말 그대로, 1차 미분만 사용하는 방법이 이런 리만공간의 업데이트엔 적합하지 않다는게 이 논문이 말하고 싶어하는 바이다. 그렇기 때문에 리만공간의 특징을 이용해 gradient를 구해 업데이트를 하자는 것이 이 논문의 목표이다.
    • 여기까지 설명하지 않아도 설명할 수 있기 때문에 생략
      • 매니폴드란, 지역적으로 point들의 거리가 euclidean한 topological space을 칭한다.
      • topological space는 set of points이고, neighborhood는 어떤방향으로 가도 set을 떠나지않고서 닿을 수 있는 point들의 집합이다.
• 그렇다면 어떻게 업데이트 할 것인가?

  • 바로, 리만 공간의 미소공간은 유클리드함을 이용한다. 먼저, 미소 공간에서의 i 번째 기저에 따른 기울기를 구하면 다음과 같다.

    \[e_i = \frac{f(x_1+dx_i) - f(x_1)}{dx_i}\]

    이를 이용한 일차 근사는 다음과 같다.

    \[ds = f(\mathbf{x}+\Delta) \approx f(\mathbf{x}) + \frac{\partial f}{\partial x_1}dx_1 + \frac{\partial f}{\partial x_2}dx_2 + ...+ \frac{\partial f}{\partial x_n}dx_n\]

    이를 위에서 정의했던 \(e_i\)로 치환하면 다음과 같다.

    \[\approx e_1 dx_1+e_2dx+...+e_ndx_n\]

    그렇다면, 어떠한 미소거리 \(\left \| ds \right \|^2\)는 다음과 같이 정의할 수 있다.

    \[\left \| dx\right \|^2 = dx \cdot dx = (e_1 dx_1+e_2dx+...+e_ndx_n)(e_1 dx_1+e_2dx+...+e_ndx_n ) \\= \sum^{n}_{i=1}\sum^{n}_{j=1}{g_{ij}dx_idx_j}\]

    이때, \(g_{ij}\)를 행렬 \({G}\)로 나타낼 수 있다. 이 행렬 \(G\)를 quadratic form으로 나타내어 본다면, \(dx^TGdx\)로 나타낼 수 있다. 이를 이용해 steepest descent방향을 구하기 위해,(업데이트를 위해 ascent할 것이지만) 행렬 \(G\)는 positive-definite matrix로 나타내는 것이 compatiable하다고 볼 수 있다. 왜냐면 positive definite일 때, \(dx^TGdx>0\)이고, 극소점이 발생하기 때문이다.

• 위를 통해 리만 공간에서 미소거리를 구하는 법을 살펴보았다. 그렇다면, 가장 steepest한 방향은 어디일까?
  • 유클리드 공간에서 가장 steepest한 방향은 기울기 (반대)방향이었다. 이를 응용해 리만 공간에서는 Lagrangean method를 통해 구할 수 있다. 먼저, 미소 거리를 \(\epsilon\)로 둔다. 유클리드 공간에서의 steepest한 vector를 잡을때 처럼, 이 증명에서도 steepest unit vector \({a}\)를 정의한다. 어떤 parameter \(w\)에 의해 정의된 함수 \(f(w)\)가 있을 때, 미소거리에서의 \(w\)에 의한 변화량 \(dw\)는 \(dw = \epsilon {a}\)이다. 그렇다면 \(f(w+dw) = f(w) + \nabla f(w)^T dw\)(유클리드공간 미분정의)가 최소이므로, \(f(w+dw) = f(w) + \epsilon\nabla f(w)^T a\)이다. 이때 \(\left \| a \right \|^2 = 1\)이므로, Lagrangean method를 사용하면, \(\left \| a \right \|^2 = 1\)를 만족하면서 \(\nabla f(w)^Ta\) 최소화 시키는 \(a\)를 찾으면 된다. 그렇기 때문에, \(\frac{\partial}{\partial a}\{ \nabla f(w)^Ta - \lambda a^T Ga\} = 0\)을 만족시키는 \(a\)를 찾으면 되는데 일단 미분이 바로 가능하므로 미분하면, \(\nabla f(w) = 2\lambda Ga\)임 을 알 수 있다. 그렇기 때문에 \(a\)는 \(a = \frac{1}{2\lambda}G^{-1}\nabla f(w)\)로 정의할 수 있다. 결국 유클리드 공간에서의 기울기에서 리만공간의 basis에 대한 변형에 비례하는 matrix \(G\)에 대한 역행렬을 곱해준 것과 같다.
  • 이때 논문에서는 policy space에서의 metric tensor \(G\)에 대한 근사로 parameter space와 policy space사이에 대한 관계를 mapping하는 역할에 fisher information matrix(FIM)를 선택했다. 이는 당연한 선택으로 보이는데, positive-definite matrix이고, parameter independent하며, 어떤 분포를 approximation하는것엔 Talyer series보다 log가 더욱 정확하기 때문이다. 또한 function compatible도 간단한 조건을 취해 쉽게 유도해낼 수 있다.
• 지금까지 policy를 어떻게 optimize하는 것이 좋을까에 대한 얘기를 했다. 다음은 어떤 조건에서 가능한지(compatible), policy iteration을하면서 얻는 action에 대한 얘기를 한다.

  • 위에서 설명했듯이 Natural Policy Gradient도 Compatible Q approximation function \(f\)를 정의하는데 Policy Gradient에서 보여준 내용과 크게 다르지 않다. 다만, policy gradient에서 조건이 하나 더 추가되는데, function \(f\)가 \(\psi^\pi(s,a) = \nabla \log\pi(a;s,\theta)\)일 때, \(f^\pi(s,a;\omega)= \omega^T\psi^\pi(s,a)\)라는 조건을 하나 더 만족해야 한다. 이는 FIM을 유도하기 위함인데 다음과 같다.

    \(\sum_s{\rho^\pi(s)}{\pi(a;s,\theta)\psi^\pi(s,a) [f_w(s,a) - Q^\pi(s,a)]} = 0\) \(\sum_s{\rho^\pi(s)}{\pi(a;s,\theta)\psi^\pi(s,a) [\psi^\pi(s,a)^T{\omega}- Q^\pi(s,a) ]} = 0\) \(\sum_s{\rho^\pi(s)}{\pi(a;s,\theta)\psi^\pi(s,a)\psi^\pi(s,a)^T{\omega}} = \sum_s{\rho^\pi(s)}{\pi(a;s,\theta)\psi^\pi(s,a) Q^\pi(s,a)}\) \(F(\theta)\omega = \sum_s{\rho^\pi(s)}{\pi(a;s,\theta)\psi^\pi(s,a) Q^\pi(s,a)}\) \(F(\theta)\omega = \nabla \eta(\theta)\) \((\because \nabla \eta(\theta) = \sum_s{\rho^\pi(s)}{\pi(a;s,\theta)\psi^\pi(s,a) Q^\pi(s,a)} = \sum_s{\rho^\pi(s)}{\nabla\pi(s,a) Q^\pi(s,a)})\) \(\omega = F(\theta)^{-1}\nabla\eta(\theta)\)

    로 나타낼 수 있고 이는 natural policy gradient update식과 같다.

• 그 다음으로, 이러한 policy가 non-covarient할 때의 그저 better action을 선택하는 것을 비판하고, covarient할 땐 best action을 선택할 수 있고, line search등의 optimization 방법과 결합하여, policy를 improve할 수 있음을 설명한다.
  • policy가 exponential family일 때에 대해 증명하는데 이는 geometrically affine properties를 가진다. 그래서 tangent vector에 의해 transformated된 point도 여전히 같은 manifold에 위치한다. 여기서는 엄밀히는 꼭 tangent vector에 의한 변화가 같은 manifold에 위치하지 않아도 된다고 한다지만 geometrical하게 이해되지는 않는다.
  • \(\pi(a;s,\theta) \propto \exp(\theta^T\phi_{sa}), \tilde{\nabla}\eta(\theta) \neq0\) 일때, gradient ascent할 양에 대한 상수 \(\alpha\)를 infinity로 보내면,(\(\pi_\infty(a;s) = \lim_{\alpha \rightarrow \infty}\pi(a;s,\theta+\alpha \tilde\nabla\eta(\theta))\)) action \(a\)는 \(f^\pi(s,a'\tilde{\omega})\)를 최대화 하는 action이 아니면 \(\pi_\infty(a;s) = 0\)이 된다.
  • \(\pi(a;s,\theta) \propto \exp(\theta^T\phi_{sa})\)이므로, \(\pi(a;s,\theta+\alpha\tilde{\eta}(\theta)) \propto \exp(\theta^T\phi_{sa}+\alpha\tilde{\eta}(\theta)^T\phi_{sa})\)이고, \(\tilde{\eta}(\theta) \neq 0\) 이므로, \(\alpha\)가 infinity로 갈 때, \(\tilde{\eta}(\theta)^T\phi_{sa}\)가 dominate하게 되므로, \(\pi_\infty(a,s) = 0\)이면 \(a \notin \mathrm{argmax}_{a'}\tilde{\nabla}{\eta}(\theta)^T\phi_{sa}\)이다.

  • 이때, \(f^\pi(s,a;\tilde\omega) = \omega^T\psi^\pi(s,a)=\tilde\nabla\eta(\theta)^T\psi^\pi(s,a)\)이고, policy가 exponential family라는 것과 function compatible조건을 이용하면, (잘 기억이 안나면, gibbs distribution에서 function \(f\)를 도출해낸 것을 다시 본다.) \(\psi^\pi(s,a)=\phi_{sa}-\mathbb{E}_{\pi(a';s,\theta)}(\phi_{sa'})\)로 정리 가능하다. 그러므로 \(f^\pi\)를 최대화 시키는 action \(a\)는 다음과 같다.

    \[\mathrm{argmax}_{a'}f^\pi(s,a';\tilde{\omega}) = \mathrm{argmax}_{a'}\tilde{\nabla}\eta(\theta)^T\phi_{sa'} - \mathbb{E}_{\pi(a';s,\theta)}(\phi_{sa'})\]

    이 때 expectation term은 \(a\)에 대한 값이 아니므로, 없애면 다음과 같다.

    \[\mathrm{argmax}_{a'}f^\pi(s,a';\tilde{\omega}) = \mathrm{argmax}_{a'}\tilde{\nabla}\eta(\theta)^T\phi_{sa'}\]

    위에서 \(\pi_\infty(a,s) = 0\)이면 \(a \notin \mathrm{argmax}_{a'}\tilde{\nabla}{\eta}(\theta)^T\phi_{sa}\)임을 보았으므로, 이를 이용하면 action \(a \in\mathrm{argmax}_{a'}f^\pi(s,a';\tilde{\omega})\) 는 \(\pi_\infty(a;s) = 0\)이 된다는 것을 알 수 있다.

  • 이 증명은 non-covarient 할 때는 오직 better action을 구할 수 밖에 없다는 것을 강조하기 위한 증명이다. 엄밀히 왜인지는 조금 생각해봐야함. 정확한 이유는 아니지만 \(\nabla\rho(\nabla\eta)\)의 방향에 대해 expectation을 사용해 구하기 때문에(\(f^\pi(s,a;\tilde{\omega}) > \mathbb{E}_{\pi(a';s)}\{f^\pi(s,a';\tilde{\omega}\}\)) best action이 선택되지 않아도 된다는 점을 본 것 같다.
• 다음으론 general한 상황에서의 정의를 보이는데, 증명은 쉬우니까 생략한다. \(\pi\)가 \(f\)를 증가시키는 방향으로 update됨을 볼 수 있는 정의이다. greedy action selection은 general하게 policy를 update시키진 못하지만 여러 optimization method와 함께 사용한다면 policy improvement를 이끌 수 있다는 내용이다.
• Metric에 대해 FIM외에 다른 metric에 대한 가능성에 대해 얘기하고 Hessian과의 관계, Cramer-Rao bound, asymptotically efficient에 대한 얘기를 하는데, 너무 설명이 길어져서 생략하고 유튜브 링크를 남긴다.
  • 링크1
  • 링크2

• 마지막으로, Natural Policy Gradient의 알고리즘은 다음과 같다.

  

  2.의 \(\nabla\mathcal{L}(\theta)\) 는 \(\nabla\mathcal{L}(\theta) =\nabla\eta(\theta) = \sum_{s,a}{\rho^\pi(s)\nabla\pi(a;s,\theta)Q^\pi(s,a)}\)로, 이에 대해 4.에서 covarient하게 \(\tilde{\nabla}\mathcal{L}(\theta) =F^{-1}\nabla_\theta\mathcal{L}(\theta)\) 로 업데이트하게 되어 5.를 진행한다. 이때, 다음과 같이 normalize시킨 step size를 이용할 수 있다. 복잡해보이지만, \(\nabla\mathcal{L}(\theta) = g\)로, 리만 공간에서의 업데이트하는 양의 크기를 분모에 넣은 것 뿐이다.

  

References

• A Natural Policy Gradient