Abstract
- GAN같은 Adversarial learning method는 현재 많은 분야에서 적용되어 사용되고 있지만, 학습 과정중 불안정한 학습을 보일 때가 있습니다.
이는 이전의 연구에서 discriminator의 성능이 너무 좋을 경우(복잡한 task일수록 discriminator가 먼저 실제 데이터와 생성된 데이터간의 차이를 빠르게 학습하는 것이 당연하므로) generator의
학습에 informative하지 않은 것을 보였습니다. 그렇기 때문에 이번 연구에서는 information bottle-neck을 통해 discriminator의 정보량을 제한하는 간단하면서 범용적인 테크닉을 소개합니다.
이는 observation과 discriminator의 internal representation 사이의 상호 정보량을 제한하는데 이는 discriminator의 성능을 유지하면서 generator에게 informative gradient를 전달하게 됩니다.
상호 정보량을 제한하는 방법으로 Variational Discriminator Bottleneck(VDB)를 사용하는데 이를 세가지 응용 케이스로 나누어 설명합니다.
- 첫번째로, imitation learning에,
- 둘째로, reward function을 재학습할 수 있는 방법에 대해,
- 셋째로, image generation에 대해 이야기를 합니다.
3. Introduction
-
이번 섹션에서는 이 논문의 기본 아이디어인 variational information bottleneck연구에 대해 review합니다. 우리는 어떤 features에 대한 데이터 \(x_i\) 그에 상응하는 labels \(y_i\)가 있다고 가정할 때, maximum likelihood estimate \(q(y_i \mid x_i)\) 는 다음을 따라 구할 수 있습니다.
\[\min_q\mathbb{E}_{x,y \sim p(x,y)}[-\log{q(y\mid x)}] \cdots (1)\]보통 \(\max_\theta f(X \mid \theta)\) 로 알고있는 form과 같습니다. 여기서 discriminator가 discriminative features에만 집중하도록 information bottleneck을 만들었는데, 이는
- features \(x\)를 latent distribution에 mapping하는 encoder \(E(z\mid x)\)와
- 상호 정보량에 대한 upper bound로 이루어져 있습니다.
이 regularized objective \(J(q,E)\) 에 대해 다시 objective를 정리하면 다음과 같습니다.
\(J(q,E) = \min_{q,E} \mathbb{E}_{x,y \sim p(x,y)}[\mathbb{E}_{z\sim E(z\mid x)}[-\log{q(y \mid z)}]]\) \(\mathrm{s.t.} I(X,Z) \leq I_c \cdots (2)\)
상호 정보량은 다음과 같이 정의됩니다.
\[I(X,Z) = \int{p(x,z)\log\frac{p(x,z)}{p(x)p(z)}d\mathrm{x}d\mathrm{z}} = \int p(x)E(z|x)\log{\frac{E(z\mid x)}{p(z)}d\mathrm{x}d\mathrm{z}} \cdots (3)\]\(p(x)\)는 dataset에서의 주어진 데이터에 대한 분포입니다. 상호정보량에서의 \(p(z)\)는 \(\int{E(z \mid x)p(x)d\mathrm{x}}\)로, 구하는 것이 어렵습니다. 그렇기 때문에, 이보다 작은 lower bound를 통해 식을 optimize하는데, 어떠한 분포 \(r(z)\)에 대해 항상 성립하는 두 가지 성질이 있습니다.
\[\mathrm{KL}[p(z) \mid \mid r(z)] \geq 0 ,\ \ \int {p(z)\log{p(z)}d\mathrm{z}}\geq \int{p(z)\log{r(z)} d\mathrm{z}}\]그러므로, (3)에서의 식은 다음과 같이 부등호로 나타낼 수 있습니다.
\[I(X,Z) \leq \int{p(x)E(z \mid x) \log \frac{E(z \mid x)}{r(z)} d\mathrm{x} d \mathrm{z}} = \mathbb{E}_{x\sim p(x)}[\mathrm{KL}[E(z \mid x) \mid \mid r(z)]] \cdots (4)\]그리고 이를 통해 얻는 objective \(\tilde{J}(q,E)\)에 관해 이전의 objective와의 관계도 \(\tilde{J}(q,E) \geq J(q,E)\)로 나타낼 수 있습니다.
\(\tilde{J}(q,E)\)에 관해 다시 (2)를 구하면 다음과 같습니다.
\(\tilde{J}(q,E) = \min_{q,E} \mathbb{E}_{x,y \sim p(x,y)}[\mathbb{E}_{z\sim E(z\mid x)}[-\log{q(y \mid z)}]]\) \(\mathrm{s.t.} \mathbb{E}_{x \sim p(x))}[\mathrm{KL}[E(z \mid x) \mid \mid r(z)]] \leq I_c \cdots (5)\)
이때 Lagrangian relaxation을 이용해 식을 변형하면 다음과 같습니다.
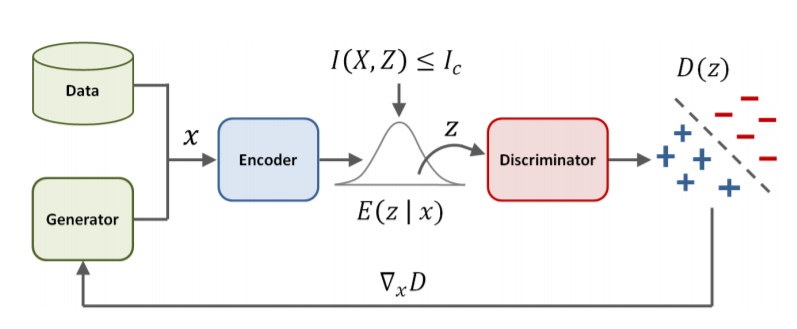
\(\min_{q,E} \mathbb{E}_{x,y \sim p(x,y)}[\mathbb{E}_{z\sim E(z\mid x)}[-\log{q(y \mid z)}]]+\beta(\mathbb{E}_{x \sim p(x)}[\mathrm{KL}[E(z\mid x)\mid \mid r(z)]]- I_c)\cdots (6)\) 마지막으로 그림을 보고 넘어가도록 하겠습니다.
4.Variational Discriminator BottleNeck
-
다음으로 실제 데이터 분포\(p^*\)와 generator에 의해 만들어진 데이터의 분포 \(G(x)\)에 대한 GAN의 loss function을 보면 다음과 같습니다.
\[\max_G\min_D \mathbb{E}_{x \sim p^*(x)}[-\log(D(x))] + \mathbb{E}_{x\sim G(x)}[-\log(1-D(x))]\]이 때, descriminator에 encoder E를 도입하고, 상호정보량에 제한을 걸면 섹션 3에서 유도되는 과정과 비슷하게 다음과 같은 식을 얻을 수 있습니다.
\[J(D,E) = \min_{D,E} \mathbb{E}_{x \sim p^*(x)}[\mathbb{E}_{z \sim E(z \mid x)}[-\log{(D(z))}]]\] \[+ \mathbb{E}_{x\sim G(x)}[\mathbb{E}_{z\sim E(z\mid x)}[-\log(1-D(z))]]\] \[+ \mathrm{s.t}\ \ \mathbb{E}_{x\sim \tilde{p}(x)}[\mathrm{KL}[E(z \mid x )\mid \mid r(z)]] \leq I_c \cdots (7)\]\(\tilde{p} = \frac{1}{2}p^* + \frac{1}{2} G\)를 가지고 상호 정보량을 제한합니다. (5)에서 (6)으로 넘어간 것과 같이 이를 다음과 같이 나타낼 수 있습니다.
\[J(D,E) = \min_{D,E}\max_{\beta \geq 0} \mathbb{E}_{x \sim p^*(x)}[\mathbb{E}_{z \sim E(z \mid x)}[-\log{(D(z))}]] +\] \[\mathbb{E}_{x\sim G(x)}[\mathbb{E}_{z\sim E(z\mid x)}[-\log(1-D(z))]]\] \[+\beta(\mathbb{E}_{x\sim \tilde{p}(x)}[\mathrm{KL}[E(z \mid x )\mid \mid r(z)]]- I_c) \cdots (8)\]이때 \(\beta\)는 Discriminator를 학습시킬 때 다음과 같이 update함으로써 (8)을 (10)과 같이 표현할 수 있습니다.
\[\beta \leftarrow \max(0,\beta + \alpha_\beta(\mathbb{E}_{x \sim \tilde{p}(x)}[\mathrm{KL}[E(z \mid x) \mid \mid r(z)]]- I_c)) \cdots (9)\] \[J(D,E,\beta) = \mathbb{E}_{x \sim p^*(x)}[\mathbb{E}_{z \sim E(z \mid x)}[-\log{(D(z))}]] + \mathbb{E}_{x\sim G(x)}\] \[[\mathbb{E}_{z\sim E(z\mid x)}[-\log(1-D(z))]]\] \[+\beta(\mathbb{E}_{x\sim \tilde{p}(x)}[\mathrm{KL}[E(z \mid x )\mid \mid r(z)]]- I_c) \cdots (10)\]이 논문에서는 \(p(z)\)의 lower bound \(r(z)\) 에 대하여 \(r(z) = \mathcal{N}(0,I)\)를 사용 하였으며, Encoder는 \(E(z \mid x ) \mathcal{N}(\mu_E(x),\sum_E(x))\) 로 표현하였습니다.
그리고 \(p^*\)과 \(G(x)\)의 수는 동일하게 뽑아 학습하였습니다.
Generator의 objective는 다음과 같이 Discriminator보다 단순합니다.
\[\max_{G} \mathbb{E}_{x \sim G(x)}[-\log{(1-D(\mu_E(x)))}] \cdots (11)\]KL penalty를 뺐고, discriminator에 들어가는 값으로 mean값만 output으로 가지면 됩니다. discriminator는 single linear unit으로 만들어졌습니다.
4.1 Discussion and Analysis
-
VDB의 효과를 해석하기 위해서는 이전의 Arjovsky의 Wasserstein GAN연구를 보아야하는데, discriminator가 optimal할 때, generator로 가는 gradient가 미약한 것을 보았습니다. 이러한 문제점을 해결하기 위해 이전에 연구에서는 discriminator의 input에 noise를 넣어주는 방법으로 해결한 연구가 있으나, 현실적으로 두 분포가 어차피 충분히 다르다면 이것으로는 부족합니다. noise의 variance를 조절하는 방법도 있으나 이도 세심히 진행되야 합니다.
-
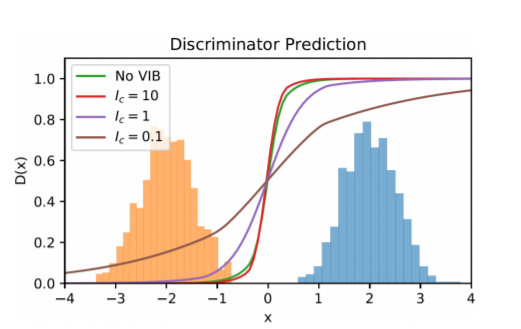
이 연구에서는 encoder가 input을 embedding으로 mapping하고, 그 embedding에 information bottleneck을 사용하는 첫 연구로써 동적으로 분포가 overlap될 수 있도록 noise의 variance를 조절합니다.(처음엔 이 말이 이해가 안됐는데, data와 generated data사이의 상호정보량을 최소화(제한)하려고 함으로써 분포가 완전히 disjoint하더라도 정보량이 제한되었으니 discriminator의 성능이 제한되고, Discriminator dominance할 확률이 줄어듭니다.) 이는 다음의 그림을 보면 쉽게 이해할 수 있습니다. \(I_c\)가 제한될수록, decision boundary가 smooth해짐을 볼 수 있습니다.
4.2 VAIL : Variational Adversarial Imitation Learning
-
(10)의 수식에서 분포를 expert 와 agent의 distribution으로만 바꾸면 다음의 수식과 같습니다. \(J(D,E) = \min_{D,E}\max_{\beta \geq 0}\mathbb{E}_{s \sim \pi^*(s)}[\mathbb{E}_{z \sim E(z \mid s)}[-\log{(D(z))}]]\) +
\[\mathbb{E}_{s\sim \pi(s))}[\mathbb{E}_{z\sim E(z\mid s)}[-\log(1-D(z))]]\] \[+\beta(\mathbb{E}_{s\sim \tilde{\pi}(s)}[\mathrm{KL}[E(z \mid s)\mid \mid r(z)]]- I_c) \cdots (12)\]이 때 agent의 reward는 \(r_t = -\log{(1-D(\mu_E(s))}\)로 계산합니다.
4.3 VAIRL : Variational Adversarial Inverse Reinforcement Learning
-
GAIL의 form을 가져와서 Adversarial Inverse Reinforcement Learning를 하면, 다음과 같이 discriminator term만 변형하여 VAIRL로 응용할 수 있습니다. \(D(s,a,s') = \frac{\exp{(f(s,a,s'))})}{exp(f(s,a,s'))+\pi(a \mid s)} \cdots (13)\) 이 때, \(f\)는 \(f(s,a,s') = g(s,a) + \lambda h(s') -h(s)\)로, trainable \(g,\ f\)로 구성됩니다. 이 때, Learning Robust Rewards with Adversarial Inverse Reinforcement Learning 의 연구에서는 \(g(s,a)\)를 \(s\)에 의해서만 정의하여 optimal \(g(s)\)는 expert의 실제 reward function를 찾을 수 있음을 증명하였습니다. 이렇게 학습한 reward에 대해서 다른 dynamics에서 학습하더라도 expert의 실제 reward로 학습한 policy와 같은 policy를 만들어 낼 수 있습니다. VAIRL에서는 (13) 을 stochastic encoder \(E_g(z_g \mid s), \ E_h(z_h \mid s)\)와 encoder에 의해 변형된 term \(g(z_g),\ h(z_h)\) 를 사용해 다음과 같이 나타낼 수 있습니다.
\[D(s,a,z) = \frac{\exp(f(z_g,z_h,z'_h))}{\exp(f(z_g,z_h,z'_h))+\pi(a \mid s)}\]Objective 는 다음과 같이 나타냅니다.
\(J(D,E) = \min_{D,E}\max_{\beta \geq 0}\mathbb{E}_{s,s' \sim \pi^*(s)}[\mathbb{E}_{z \sim E(z \mid s,s')}[-\log{(D(s,a,z))}]] +\) \(\mathbb{E}_{s,s'\sim \pi(s,s'))}[\mathbb{E}_{z\sim E(z\mid s,s')}[-\log(1-D(s,a,z))]]\) \(+\beta(\mathbb{E}_{s,s'\sim \tilde{\pi}(s,s')}[\mathrm{KL}[E(z \mid s,s')\mid \mid r(z)]]- I_c)\)
이 때, 세부 표기는 다음과 같습니다.
\(z = (z_g,z_h,z'_h),\\ \ \ f(z_g,z_h,z'_h) = D_g(z_g) + \lambda D_h(z'_h) - D_h(z_h)\)
\(\ \mathrm{and}\ E(z \mid s,s') = E_g(z_g \mid s) \cdot E_h(z_h \mid s) \cdot E_h(z'_h \mid s')\)