Abstract
- 실제 상황에서는 decentralized된 방법으로 행동해야하지만, 학습할 때는 centralized하게 학습시킬 수 있는 경우에 대해 이 논문은 설명합니다. decentralized와 centralized training way에 대해 이전에 설명해놓은 링크를 남깁니다. 하지만 centralized하게 학습시켰을 때, 어떻게 decentralized policy를 추출하는지에 대해 생각해 보아야 하는데, 이 논문이 QMIX라는 방법을 통해 해결하게 됩니다. 이 QMIX는 뒤에서 자세하게 설명하도록 하겠습니다.
Introduction
- 이 논문의 베이스가 되기도 하지만 많은 MARL 방법론에서는 Centralized Training with Decentralized Execution 방식을 취하고 있습니다. 하지만 이 방법론에 있어서 가장 중요한 점은 어떻게 centralized하게 학습시킨 policy를 decentralized execution에 이용하느냐 입니다. 예를들면 global state에 접근가능한 Q인 \(Q_{tot}\)를 학습한다고 가정하면, 이는 모든 joint action과 state들에 대해 학습을 했을 것입니다. 그렇다면 이를 decentralized policy에 이식할 수 있을까요?
- 가장 간단한 방식으로는 \(Q_{tot}\)를 사용하는게 아닌, 각자의 observation만을 보고 학습하는 Independent Q learner를 학습시키는 것입니다. 이리하여 각 agent는 각자의 학습에 있어 environment로만 여겨지게 됩니다. 하지만 이 방법은 다른 agent의 행동에 따라 dynamics가 변하게 되므로, 불안정합니다.(신기하게 어느정도 학습이 되는 모습은 보여, 벤치마크로 자주 이용되고 있습니다.)
- 다른 방법으로, COMA의 방식이 있는데 이도, 이전에 설명해 놓은 링크를 따라가시면 section 3에서 확인하실 수 있습니다. 간단히 centralized \(Q_{tot}\)를 이용해 decentralized policy를 학습시키는 방법입니다. 이 방법은 on-policy이므로 sample-inefficient하고, 모든 agent 숫자 만큼의 value network input을 가지므로 agent가 많으면 많을수록 커버하기 힘들어집니다.
- 이러한 두가지 극과 극을 보았는데, 이번엔 Value Decomposition Network(VDN)을 통한 방법을 보도록 하겠습니다. \(Q_{tot}\)는 각자의 value function \(Q_a\)의 합으로써, agent는 모두 각자의 local observation만을 사용하여 \(Q_a\)를 추론합니다. 하지만 VDN은 centralized training중의 많은 정보들을 포기할 수밖에 없습니다.
-
그렇기 때문에 이 논문에서는 QMIX라는 방법을 소개하는데, 핵심 아이디어는 이런 VDN의 구조가 decentralized policies를 구하는데 필수가 아니라는 점에서 시작합니다. 대신 \(Q_{tot}\)로 구한 global argmax가 각자의 \(Q_a\)의 argmax와 같도록 학습하게 됩니다. 이때 \(Q_{tot}\)와 \(Q_a\)는 다음과 같은 간단한 monotonicity constraint만 만족하면되는데, 이는 다음과 같습니다.
\[\frac{\partial Q_{tot}}{\partial Q_a}\geq, \ \forall a \cdots (1)\]이를 만족하여야하는 이유는 Appendix에 나오긴 하지만 간단하게 말하자면, 이렇게 업데이트가 되어야 argmax로 개인의 agent를 update하는 행위가(\(Q_a\)의 증가가), 전체의 \(Q_{tot}\)의 증가로 이루어지기 때문입니다.
또한, QMIX는 이러한 agent networks들의 집합 \(Q_a\)와 mixing network가 존재하는데 이는 \(Q_a\)들을 \(Q_{tot}\)로 묶어줄 때, VDN처럼 그냥 더하는 것이 아닌, neural network를 거쳐 각자의 \(Q\)에 대한 비선형성을 만들어 줍니다. 이 mixing network는 positive weights만 가지도록 제한되는데 이는 위의 (1)의 constraints와 연관 있습니다.
Background
QMIX
-
이번 장에서는, QMIX에대해 좀더 자세하게 설명해보겠습니다. 2장에서의 설명처럼 VDN는 다음과 같이 구할 수 있습니다.
\[Q_{tot}(\mathbf{\tau},\textbf{u}) = \sum^n_{i=1}{Q_i(\tau^i,u^i;\theta^i}) \cdots (3)\]하지만, QMIX는 다음과 같이 \(Q_{tot}\)를 구성합니다.
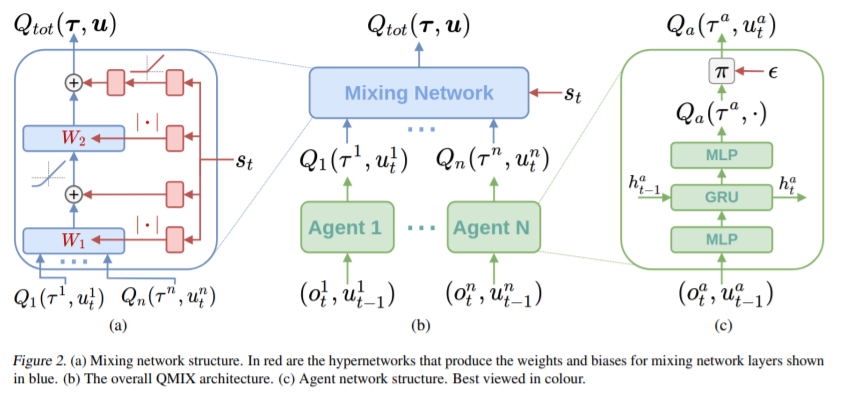
\[\mathrm{argmax}_\textbf{u}Q_{tot}(\mathbf{\tau},\textbf{u}) = \begin{pmatrix} \mathrm{argmax}_{u^1}Q_1(\tau^1,u^1)\\ \cdots \\ \mathrm{argmax}_{u^n}Q_n(\tau^n,u^n) \end{pmatrix} \cdots (4)\]VDN과 다른점은 각 \(Q_a\)가 각자의 argmax를 구하여 \(Q_{tot}\)를 구성한다는 점입니다. 그렇다면 agent는 각자의 최대 action value를 찾으면 되는데 이때문에 off-policy RL밖에 적용할 수 없습니다. QMIX를 이해하기 위해 그림을 먼저 살펴보겠습니다.
QMIX는 다음과 같이 우측부터 agent network, mixing network, 그리고 이를 이루고 있는 hypernetwork를 설명하도록 하겠습니다.
- agent network는 그림 (c)와 같이, 시점 t의 observation \(o^a_t\)와 이전의 agent의 행동 \(u^a_{t-1}\)로 이루어져 있고, network는 DRQN에서 처럼 GRU가 들어가 있습니다. 이는 POMDP등의 상황에서 자주 쓰이는 테크닉인데, MARL도 같은 맥락이기 때문에 적용이 reasonable하다고 할 수 있습니다.
- mixing network는 agent network의 output을 input으로 받아 \(Q_{tot}\)를 만듭니다. 이 때, weights들은(biases는 non-positive해도 괜찮습니다.) non-negative하지않도록 제한됩니다. 이를 어떻게 non-negative하도록하느냐를 다음의 hypernetwork가 해결합니다.
- 이러한 mixing network를 이루는 각각의 분리된 hypernetwork로 이루어져있는데, hypernetwork는 state s(global information)를 input으로받아, mixing network의 weight를 output(\(W_k\))으로 가지게 됩니다.(hypernetwork 자체가 weights를 생성하는데 사용이 되는 network입니다.) network의 각 hypernetwork는 하나의 linear layer로 되어있고, 그다음 absolute activation function를 거쳐 mixing network의 weights이 non-negative하도록 만듭니다. 이렇게 해서 나온 hypernetwork의 output은 원하는 크기의 vector가 나오게 됩니다. 이때 biases는 같은 방식으로 구할 수 있으나, non-negative하지않아도 됩니다. 마지막 bias는 2 layer with relu hypernetwork를 통해 구하는데 (a)의 상단을 보시면 설명이 되어있습니다.
-
state는 바로 mixing network에 가는 것이 아닌 hypernetwork를 거치게 되는데, 이는 추가적인 information들이 (1)을 만족해야하기 때문입니다. 결국 loss는 다음과 같이 나타낼 수 있습니다.
\[\mathcal{L} (\theta)=\sum^b_{i=1}[(y^{tot}_i - Q_{tot}(\mathbf{\tau},\textbf{u},s;\theta))^2]\] \[y^{tot}=r+\gamma \max_{u'}Q_{tot}(\mathbf{\tau}',\textbf{u}',s';\theta^-)\] - 이렇게 학습된 agent들은 mixing network없이 decentralized execution에선 agent를 그대로 사용하면 됩니다.