Abstract
- cooperative MARL의 이전 연구들에선 주로 reward-shaping혹은 centralized critic을 통해 학습하는 방법들이 많은 연구가 이루어졌습니다. 이 논문은 intrinsic reward를 도입하여 그 두가지 방향을 모두 통합하는데, 이를 위해 각 actor의 decentralized critic은 extrinsic reward만을 maximize하기 위함이 아닌 혼합된 proxy critic으로, 어떻게 이 intrinsic reward가 학습을 도울 수 있는지 뒤에서 알아보겠습니다.
Related Work
- QMIX도 그렇고, 많은 방법이 critic을 어떻게 구성하는지에 대해 고민했는데, 이 논문에서는 그것보다 intrinsic reward를 통해 그를 해결하려고 합니다. intrinsic reward는 결국 objective를 maximize하기 위한 meta data로 meta learning을 MARL에 적용한 case라고 볼 수 있습니다.
Background
Method
- The Objective
- intrinsic reward function은 \(r^{\mathrm{in}}_{\eta_i}(s_i,u_i)\)로 나타냅니다. 이 때 \(\eta_i\)는 이를 구성하는 파라미터를 나타내며 아래부터는 생략되어 사용됩니다. 위에서 설명했던 proxy critic을 구성하기 위한 proxy reward는 다음과 같습니다.
proxy value function은 다음과 같이 나타낼 수 있습니다.
\[\mathrm{V}^{\mathrm{proxy}}_{i,t}(s_{i,t}) = \mathbb{E}_{u_{u,t,s_i,{t+1}},...}[R^\mathrm{proxy}_{i,t+l}]\]원래 우리가 해결해야하는 extrinsic value function은 \(V^{\mathrm{ex}}\)로, 실제 proxy value function이 어떤 것을 의미하냐 했을 때 사실 큰 의미는 없지만 이를 통해 각 agent의 policy를 update하게 됩니다. 마지막으로 전체적인 objective를 살펴보겠습니다.
\[\max_{\mathbf{\eta},\mathbf{\theta}} J^\mathrm{ex}(\mathbf{\eta}), \\\] \[\textbf{s.t.}\ \ \theta_i = \mathrm{argmax}_{\theta}J^{\mathrm{proxy}}_i(\theta,\mathbf{\eta}),\ \ \forall i \in [1,2,\cdots,n]\]이는 proxy objective를 최대화하는 policy에 대해 intrinsic reward parameter를 조절해 extrinsic objective를 최대화하는 bilevel optimization으로 볼 수 있습니다. 이는 다시말해 각 iteration마다, policy parameter가 proxy objective를 maximize하는 방향으로 update되고, 그다음 intrinsic reward parameter가 extrinsic objective를 maximize하는 방향으로 update된다는 것을 의미합니다.
Algorithm
-
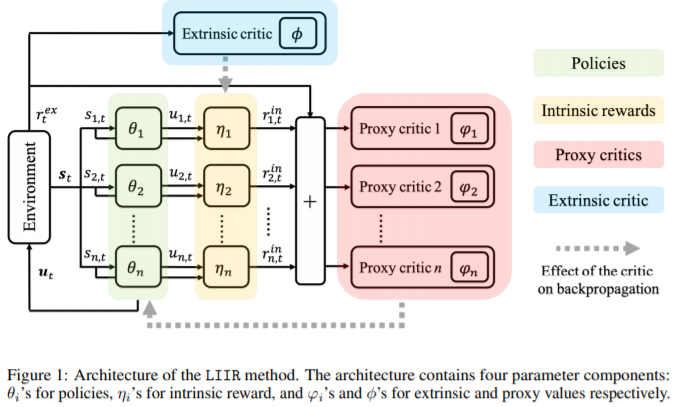
그림을 먼저 보겠습니다.
이 논문에서는 간단하게 REINFORCE algorithm을 적용합니다. environment부터 flow를 살펴보자면, environment로부터 state을 받은 각 agent는 action을 취하고 extrinsic critic이 intrinsic reward를 주면 그를 가지고 proxy critic을 통해 얻은 advantage function을 가지고 actor를 update합니다. 이는 다음과 같이 수식으로 나타낼 수 있습니다.
\[\nabla_{\theta_i}\log\pi_{\theta_i}(u_i|s_i)A^{\mathrm{proxy}}_i(s_i,u_i) \cdots (6)\]그렇다면 intrinsic reward는 어떻게 update될까요? 바로 policy extrinsic objective를 intrinsic reward parameter \(\eta\)로 편미분해 gradient ascent를 해주면 됩니다. 이때 intrinsic reward에 대한 extrinsic objective의 변화량은 policy parameter변화량에 의존하기 때문에 chain rule을 통해 다음과 같이 나타낼 수 있습니다.
\[\nabla_{\eta_i}J^{\mathrm{ex}} = \nabla_{\theta'_i}J^{\mathrm{ex}}\nabla_{\eta_i}\theta'_i \cdots (7)\]이를 둘로 나누어 보면, \(\nabla_{\theta'_i}J^\mathrm{ex}\)와 \(\nabla_{\eta_i}\theta'_i\)로 나타낼 수있고, 첫번째 부터 보자면, 이미 update된 policies에 대한 parameter \(\theta'\)에 대해 distribution이 바뀌었으므로, 새로운 sample을 뽑거나 Importance sampling을 통해 이를 다음과 같이 나타냅니다.
\[\nabla_{\theta'_i}J^\mathrm{ex} = \nabla_{\theta'_i}\log\pi_{\theta'_i}(u_i|s_i)A^\mathrm{ex}(\textbf{s},\textbf{u})\]다음으로 \(\nabla_{\eta_i}\theta'_i\)는 다음과 같이 나타낼 수 있습니다.
\[\nabla_{\eta_i}\theta'_i=\nabla_{\eta_i}[\theta_i+\alpha\nabla_{\theta_i} \log{\pi_{\theta_i}}(u_i|s_i)A^{\mathrm{proxy}_i(s_i,u_i)}]\]이 때, 앞의 term은 reward parameter에 변화에 따른 policy parameter의 변화율은 연관이 없으므로 없어지게 되고, 뒤의 term만 남게되는데 이는 다음과 같이 정리됩니다.
\[= \alpha\nabla_{\theta_i} \log{\pi_{\theta_i}}(u_i|s_i)\nabla_{\eta_i}r^\mathrm{proxy}_i(s_i,u_i) \cdots (9)\]이를 알고리즘으로 확인해보면 위의 설명대로 진행됨을 알 수 있습니다.