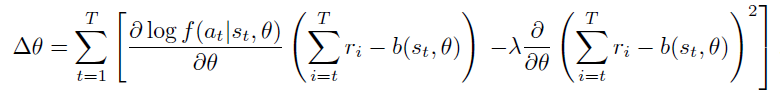Abstract

  • 이 논문은 unsuperviesd learning을 통해 agent가 environment에 대해 배울 수 있는 방법에 대해 설명합니다. 독특한 점은 이 방법을 쉽게 설명하기 위해 등장하는 두 성격의 agent를 Alice와 Bob으로 이름붙여 소개하는데 이어서 설명하도록 하겠습니다.

Introduction

Approach

  • Alice와 Bob은 물리적으로는 같은 agent에서 교대로 등장합니다. 이 때, Alice는 Bob이 해결해야할 문제를 제시해주고, Bob은 이를 해결하는 역할을 하는데, environment에 따라 이 교대 방법을 두 가지를 사용할 수 있습니다.
    • 첫 째로, Alice가 한 시작 시점 \(s_0\)에서 출발하여 Stop action이 나오면 그대로 Bob은 거기서부터 원래 시작 지점 \(s_0\)까지 돌아오는 방식

    • 둘 째로, Alice가 한 시작 지점 \(s_0\)에서 출발하여 Stop action이 나오면 Bob은 처음부터 그 지점 \(s^*\)까지 이동하는 방식

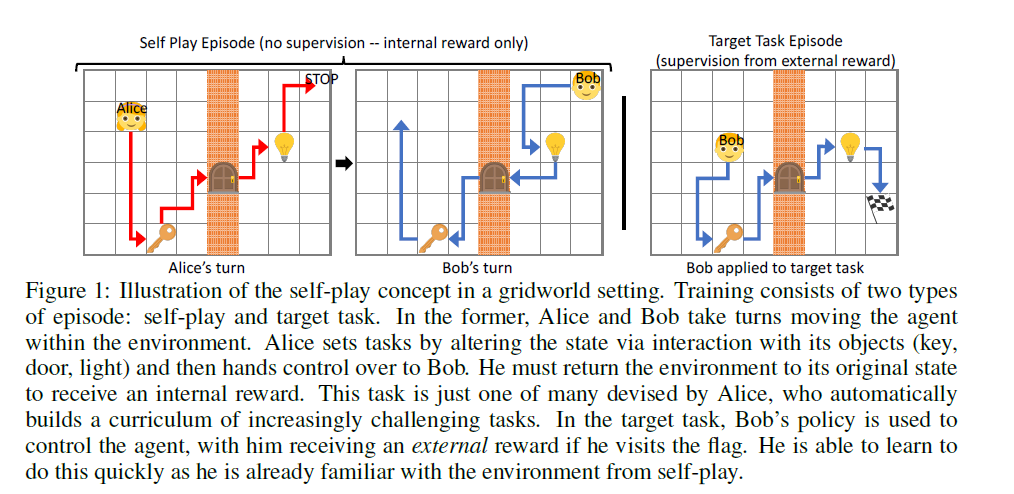
      Alice와 Bob은 같은 network 구조를 가지지만, 다른 parameter를 가진 채 학습됩니다. 그림을 통해 먼저 설명하겠습니다.

      auto self play

      training은 방금 설명한 방식의 self-play와 실제 해결하고 싶은 문제 target task로 이루어 집니다. self-play는 target task의 reward가 아닌 intrinsic reward를 가지는데, 이는 Bob이 target task학습하는데 도움을 주게 됩니다. 이 논문에서 intrinsic reward에 대한 설정으로 Bob은 Alice이 제시한 task를 빠르게 달성하는 것에만 초점을 둡니다. 그러므로 다음과 같이 설정할 수 있습니다.

      \[R_B = - \gamma t_B\]

      \(t_B\)는 task를 마치기 위해 걸린 시간입니다. 또한 Alice의 reward는 다음과 같이 설정할 수 있습니다.

      \[R_A = \gamma \max{(0, t_B - t_A)}\]

      이는 Alice가 Bob보다 느리면, 더 어려운 task를 주도록 유도되지만, Bob이 Alice보다 느리다고 쉬운 task를 주도록 유도되지는 않는다는 의미입니다. \(\gamma\)는 extrinsic reward와 scale을 맞추기 위해 사용되었습니다.

  1. Parameterizing Alice and Bob’s Action
    • Alice와 Bob은 모두 두 가지 state에 대한 observation을 받고, action에 대한 distribution을 output으로 가집니다. Alice의 function에 대해서 다음과 같이 나타낼 수 있습니다.
    \[a_A = \pi_A(s_t,s_0)\]

    Bob은 다음과 같이 나타낼 수 있습니다.

    \[a_B = \pi_B(s_t,s^*)\]

    \(s^*\)는 Bob이 이동해야할 곳의 위치입니다. 이 때, target task를 해결해야할 땐, \(s^*\)에 0 값을 넣어서 signal을 주고, self-play 중 \(s^*\)이 0이 나오는 일이 존재한다면, parameter를 하나 더 추가해서 target play라는 signal을 전달합니다. 알고리즘 상에선 이를 다음과 같이 표현합니다.

    \[\pi_A(s_t,s_0) = f(s_t,s_0,\theta_A), \ \pi_B(s_t,s^*) = f(s_t, s^*, \theta_B)\]

    설명을 바탕으로 self-play와 target task에 대한 algorithm을 보자면 다음과 같습니다.

    auto self play

    auto self play

  2. **Universal Bob in the Tabular Setting
    • finite states, tabular policies, deterministic, Markovian transition 상태에 대해 self-play를 통해 Bob이 최단거리로 이동하도록 학습된다는 것을 증명합니다.
    • Preliminaries : \(\pi_{\mathrm{fast}}(s_t,s^*)\)가 가장 빠른 step으로 간다면 이는 Bob의 ideal policy이고, Alice의 return이 0이 됩니다.
    • Claim : \(\pi_A = \pi_B\)라면, \(\pi_B = \pi_{\mathrm{fast}}\)이다.
    • Argument : \(\pi_B\)가 \(\pi_{\mathrm{fast}}\)가 아니라면, \(\pi_B\)는 \(\pi_{\mathrm{fast}}\)보다 느립니다. Bob은 \(\pi_{\mathrm{fast}}\)를 통해, 더많은 reward를 받을 수 있는데, \(\pi_A\)가 고정됐을 때, \(\pi_B\)가 평형상태라면, Alice가 challenge하지 않다는 뜻입니다. 그렇다면 \(\pi_A\)가 \(\pi_{\mathrm{fast}}\)가 나왔을 때, Alice는 positive reward를 받는데, 이는 가정에 위배되므로, claim은 참이 됩니다.
  • GAN과 같이 adversarial network와 관계가 있는데, Alice가 generator역할을 하기 때문입니다. 하지만 Bob은 discriminator라기보단 task를 완수하는 역할을 수행합니다.
  • Intrinsic motivation에도 큰 연관을 가지고 있는데, 이 중 큰 흐름인, curiousity-driven exploration과 다른 점은 Bob이 한 task를 잘 해내지 못하면 Alice는 많이 탐색한 state라도 계속해서 갈 수 있다는 점입니다. 또, Empowerment 계열의 environment를 얼마나 control할 수 있는지에 관한 exploration 전략과도 여기서는 control에 대한 measurement가 없으므로 다릅니다.
  • Curriculum learning과도 연관이 있습니다.
  • Horde architecture와도 연관이 있습니다. value function에서 goal을 받는다는 점이 다릅니다.
  • 이외에 internal state를 target으로 하는 연구, goal로 부터 점점 거리를 늘려가는 방법, random alice를 이용하는 연구들이 존재합니다.

Experiments

  • Bob과 Alice모두 baseline을 사용한 Policy gradients로 학습됩니다. 이 때, expected reward maximize외에도 baseline과 멀어지지 않도록 하는 term을 넣었습니다.

    auto self play

References