Fast Task Inference with Variational Intrinsic Successor Features 논문 리뷰 및 설명

Abstract

• Environment의 extrinsic reward없이 agent가 다양한 행동들을 배울 수 있다는 것을 기존에 보인 많은 연구들이 많습니다. 이 때 기본적인 아이디어로 policy가 다른 policies들과 구별되도록 행동 하는 것에 reward를 줌으로써 학습이 이루어졌습니다. 하지만 이 방법은 학습된 행동 집합들은 이후 task에 대해 generalization이 어렵다는 단점이 있습니다. 이와 별개로 Successor features는 Meta RL에서 reward function의 generalization을 위해 제시된 아이디어인데, 이는 reward function이 linear해야한다는 단점을 가지고 있습니다. 이 논문은 둘을 합쳐 각각의 한계를 해결한 Algorithm, Variational Intrinsic Successor FeatuRes(VISR)를 제시합니다.

Introduction

• 개인적으로 Algorithm을 보고 읽는게 쉬울 것 같아 앞에 먼저 algorithm을 남겨둡니다.

  

• Unsupervised Learning은 최근 Deep learning의 엄청난 진전을 가져온 중요한 역할을 맡고 있습니다. 다만 RL에선 Unsupervised Learning이 좀 더 복잡하게 적용될 수 밖에 없습니다. 그 방법중 하나로 intrinsic reward을 agent에게 주는 방법을 통해 좋은 state를 찾는 여러 연구들이 진행되어 왔습니다. 하지만 이외에도 unsupervised learning은 유용한 state representation와 skill을 습득하는 것 또한 해결할 수 있습니다.
• unsupervised RL은 기존 supervised learning에서 unsupervised representation learning할 때 label을 제거하듯 environment의 extrinsic reward를 제거한 뒤 행해집니다.
• 최근 unsupervised pre-training을 사용한 RL의 SOTA는 latent variable policies와 state에 따른 action간의 mutual information을 maximize(behavioral mutual information(BMI))하는 연구들이 있습니다. 하지만 이들은 generalization이 잘 안되고, reward signal이 주어졌을 때, inference가 느리다는 단점이 있습니다. 구조적인 문제로, 어떤 task에 대해 실제 필요로 하는 skill은 pre-training할때 mapping한 points사이에 존재할텐데(몇 가지 skill을 적절히 섞거나 그들 사이에 있어야하는 등) 이를 적절히 interpolate해야 한다는 문제가 남아 있습니다.
• 이 논문의 contribution으로, successor features(SF)를 통해 generalization과 slow inference problem을 둘다 해결한다는 점이 있습니다. SF는 빠른 transfer learning을 가능하게 했지만 이를 어떻게 정의해야 하는지에 대해 열린 문제로 남아있었습니다. 이 논문은 BMI를 maximize하는 것이 이 features를 학습하는 것에 대해 강력한 해답을 제공함을 보입니다.

Reinforcement learning with Unsupervised Pre-training

• 실험은 pre-training과 실제 task에 대한 test의 두 가지 stages로 구성되는데, pre-training에는 extrinsic reward를 전혀 받지 못하고, 실제 task에서는 기존 RL의 환경처럼 학습시키게 됩니다.

• RL에서의 agent는 expected return을 최대화할 수 있는 policy를 찾는 것이 goal로써, 이 문제를 해결하는 방법으로 dynamic programming에서 나온 방법을 사용하는데, 이는 value function에 크게 의존합니다. 이 때, 주어진 policy \(\pi\)에 대한 action-value function는 \(Q^\pi(s,a) \equiv \mathbb{E}^\pi[G_t|s_t = s, A_t = a]\)로 정의 할 수 있습니다. 그리하여 \(Q^\pi\)에 입각한 greedy policy는 다음과 같이 정의합니다.

  \[\pi'(s) \in \mathrm{argmax}_aQ^\pi(s,a)\cdots(1)\]

  \(\pi'\)는 최소한 \(\pi\)만큼의 성능을 내는 것이 보장되는데, 이는 다음과 같기 때문입니다.

  \[Q^{\pi'}(s,a) \geq Q^\pi(s,a),\ \ \mathrm{for\ all} (s,a) \in S \times A\]

  \(Q^\pi(s,a)\)를 optimize하는 과정을 policy evaluation, \(\pi '\)를 optimize하는 과정을 policy improvement라고 합니다. RL은 이 과정을 approximation을 사용해 학습해 나갑니다. 이 때 reward \(r(s,a,s')\)를 어떤 cumulant \(c(s,a,s')\)로 바꿔도 위의 모든 과정들은 동일한데, 이를 따르는 policy \(\pi_c(s)\)와 \(Q^*_c(s,a)\)를 나타낼 수 있습니다.(임의로 생성한 reward function 정도로 이해하셔도 됩니다. 본래 reward와는 다른 임의의(discriminator로부터나온) reward를 생성해서 사용하기 때문에 이런 표현을 사용합니다.)

• 또한 learning과정에서 environment와 interaction하면서 발생하는 cost가 있기 때문에 agent의 policy는 최대한 빨리 학습되어야하는데, 이 논문은 오직 두번째 stage에 대해서만 cost를 고려합니다. 그리하여 첫번째 stage는 두번째 stage를 얼마나 빠르게 수렴시킬 수 있는지에 대해 평가하게 됩니다.

Universal Successor Features and Fast Task Inference

• 다음과 같이 reward function을 표현할 수 있는 한 feature \(\phi (s,a,s') \in \mathbb{R}^d\) 가 존재한다고 가정합니다.

  \[r(s,a,s') = \boldsymbol{\phi}(s,a,s')^T\boldsymbol{w}\cdots(2)\]

  이 때, \(\boldsymbol{w} \in \mathbb{R}^d\)인 weights는 얼마나 각 feature가 desirable하냐에 가중치를 주는데 이를 task vector라고 부릅니다. \(\boldsymbol{\phi}\)는 아무 제약조건이 없다면 예를 들면 어떤 i에 대해서 다음의 식 \({\phi}_i(s,a,s') = r(s,a,s')\)를 만족하도록 만들면, reward는 그대로 복원될 수 있습니다. \(Q^\pi(s,a)\)는 다음과 같이 표현됩니다.

  \[Q^\pi(s,a) = \mathbb{E}^\pi[\sum^\infty_{i=t}\gamma^{i-t}\boldsymbol{\phi}_{i+1}|S_t=s, A_t = a]^T\boldsymbol{w}\]

  이는 또, successor features \(\boldsymbol{\psi}\)로 나타내면 다음과 같습니다.

  \[Q^\pi(s,a) \equiv \boldsymbol{\psi}^\pi(s,a)^T\boldsymbol{w}\cdots(3)\]

  SFs는 multi-dimensional value function으로 볼 수 있고, \(\boldsymbol{\phi}(s,a,s')\)는 reward의 역할을 하게 됩니다. SFs의 장점은 unsupervised learning 때, \(\boldsymbol{\psi}^\pi\)를 계산하면, 다음 stage에서 \(\boldsymbol{w}\)만 regression problem으로 계산하면 됩니다.

• \(\pi\)가 reward 없이 학습되므로 \(\pi'\)는 policy improvement에 의존합니다. 이 때 이를 여러 policies를 가지고 improve했을 때 좋은 성능이 나옴을 기존 Generalized policy improvement(GPI) 연구에서 보였는데, 이를 위해 policy-encoding mapping \(e : (\boldsymbol{S} →\boldsymbol{A})→\mathbb{R}^k\) 를 사용합니다. 이는 policy를 vector로 바꿔주는 역할을 합니다. 기존의 연구에서 universal successor feature(USFs)는 \(\boldsymbol{\psi}(s,a,e(\pi)) \equiv \boldsymbol{\psi}^\pi(s,a)\)로 정의되었는데, USFs를 사용하면, 이제 여러 polices를 통해 policy \(\pi\)에 대해 다음과 같이 간단하게 나타낼 수 있습니다.(policies를 다양하게 사용하는 이유에 대해 이후에 policies를 뽑는 방법에 의해 generalization에 도움이 되는 면을 보실 수 있습니다.)

  \[Q^\pi(s,a) = \boldsymbol{\psi}(s,a,e(\pi))^T\boldsymbol{w} \cdots(4)\]

  그러면 이제, 모든 \(\pi\)에 대한 \(Q^\pi\)를 구할 수 있으므로, 이를 통해 policy를 개선할 수 있어야 합니다. 이는 generalized policy improvement를 통해 업데이트 하는데 다음을 통해 가능합니다. \(\boldsymbol{\psi}\)가 USFs이고, 각 policies \(\pi_1,\pi_2, ...,\pi_n\) 에 대해,

  \[\pi(s) = \mathrm{argmax}_a\max_i\boldsymbol{\psi}(s,a,e(\pi_i))^T\boldsymbol{w} = \mathrm{argmax}_a\max_iQ^{\pi_i}(s,a) \cdots(5)\]

  로 업데이트 할 수 있습니다. 이는 (1)의 식보다 모든 policies에 대해 크므로 엄격한 generalization입니다. 이 결과는 (2)가 근사되어 활용되고, \(\psi\)가 universal successor feature approximator(USFA)로 교체되는 경우로 확장될 수 있습니다.

  이렇게 USFA에서는 unsupervised pre-training을 통해 data-effciency를 높이는 방법에 대해 제시하는데 방법은 이와 같습니다. unsupervised phase 동안, agent는 USFA \(\boldsymbol{\psi}_\theta\)를 배웁니다. 그렇게 되면, RL phase때 \(\boldsymbol{w}\)만을 근사하면 됩니다. 마지막으로 n개의 policies \(\pi_i\)와 policy \(\pi\)에 대해서 근사치가 적당히 맞다면, \(\pi\)가 improve될 것임을 보입니다.

• 그러나 아직 \(\boldsymbol{\psi}\)는 어디서 오는 것이며, \(\pi_i\)는 어떻게 정의해야하는지에대해 아직 질문이 남아있습니다.

Behavioral Mutual Information

• \(\boldsymbol{\psi}\)는 RL phase때 \(\boldsymbol{\psi}\)를 이용해 쉽게 표현될 수 있도록 정의되어야 합니다. unsupervised phase때는 task reward에 대한 정보를 전혀 얻을 수 없음을 가정했으니, inductive bias를 통해 합리적인 task의 reward와 관련있는 feature를 만들어내도록 해야합니다.
• 이러한 bias는 오직 agent가 controllable한 observation space의 부분집합으로만 이루어지므로 이는 policy conditioning variable과 agent’s의 행동에 대해 mutual information을 maximize하여 해결할 수 있습니다. (mutual information을 통해 둘 간의 불확실성을 minimize하여 state를 controllable하도록 합니다.)

• objective \(\mathcal{F}(\theta)\)는 policy를 조절하는 variable z와 policy에 의해 생성된 trajectories에 관한 function f간의 mutual information을 maximize하는 policy의 parameter \(\theta\)를 찾는 작업이고 다음과 같이 나타낼 수 있습니다. 마지막항은 mutual information 정의에 의해 entropy로 분리 가능합니다.

  \[\mathcal{F}(\theta) = I(z;f(\tau_{\pi_\theta})) = H(z)- H(z|f(\tau_{\pi_\theta}))\cdots(6)\]

• z에 대해 entropy를 maximize하기위해 fixed uniform distribution으로부터 z를 sampling 가정하여 식을 simple하게 변형하면 다음과 같습니다.

  \[\mathcal{F}(\theta) = - H(z|f(\tau_{\pi_\theta}))\cdots(7)\]

  trajectory가 충분히 길다면, state의 분포는 policy에 의해 형성되는 정상상태의 distribution이 됩니다. 이 때, \(f\)를 \(\tau_{\pi_\theta}\)에서 uniform하게 sampling하는 연산이라고 하면 (7)의 식은 다음과 같이 정리됩니다.

  \[\mathcal{F}(\theta) = \sum_{s,z}p(s,z)\log{p(z|s)} = \mathbb{E}_{\pi,z}[\log{p(z|s)}]\]

  이는 variational approximation \(q\)에 의해 lower-bounded되어 loss function으로 사용 가능한데, 간단한 정의이므로 section 8.1을 보시면 됩니다.

  이 때, 주의해야할 점은 \(\pi\)와 \(q\) 둘에 의해 loss가 정의됐다는 점입니다. 그렇다면 \(q\)는 variational parameters는 실제 분포와의 negative log likelihood를 minimizing하는 방법으로 optimization이 가능합니다. 즉, q는 z를 predict하도록 학습됩니다. 하지만 policy의 parameter \(\theta\) 는 non-differentiable environment를 통해 학습해야 하기 때문에, REINFORCE trick을 사용해 \(\log{q(z|s)}\)를 reward로, \(V_{\theta}(s) = \mathbb{E}_{\pi,z}[\sum^T_{t=0}\log{(q(z|s_t)}|s_0=s]\) 를 maximize하는 REINFORCE 수식과 동일하게 update해야합니다.

  이전 연구들은 policy \(\pi\)는 latent \(z\)위에서 skills을 보이는게 목표였습니다. 이 때 discriminator q는 \(\tau\)로부터 \(z\)를 추론하는 등 이용될 수 있으나, 이 연구에선 RL phase에서 모든 z에 대해 열어놓고 탐색하기 위해 사용하지 않습니다. 다음 section에서 unsupervised phase에서 학습한 행동을 활용하기 위해 어떤 방법을 사용하는지 설명합니다.

Variational Intrinsic Successor Features

• 이 방법은 BMI의 method와 함께 SFs에 영향을 받았습니다.
  이 두 방법은 모두 task를 parameterize하기 위해 vector를 사용한다는 점에서 시작합니다. SF에서는 주어진 task에 대해 reward 를 정의할 때 쓰이는 linear weight \(\boldsymbol{w}\)와 BMI의 objective에서는 task를 define하기 위한 z를 maximize하기 위한 reward \(\log{q(z|s)}\)를 같도록 제한하여 해결하는데, \(z \equiv \boldsymbol{w}\)가 되기 위해서는, \(r_{SF}(s; \boldsymbol{w}) = r_{BMI}(s;\boldsymbol{w})\)여야하는데,(이전 section에서의 reward와 같은형태) 이는 BMI discriminator q가 다음을 만족해야함을 의미합니다.

  \[\log{q(\boldsymbol{w}|s)} = \boldsymbol{\phi}(s)^T\boldsymbol{w}\]
• 이 조건을 만족하기 위해서는 task vector \(\boldsymbol{w}\)와 \(\boldsymbol{\phi}\)를 unit length로 맞춰야하고, discriminator q를 scale parameter가 1인 Von Mises-Fisher distribution을 따라 parameterizing해야합니다. 이는 q를 multivariate gaussian으로 parameterization을 하면 되지 않느냐도 생각할 수 있지만, Von Mises-Fisher distribution을 따라야 만족합니다.(unit length를 맞춰야 하는 것도 있지만 직관적으로도 이런 선택이 task varaible w를 명확하게 학습할 수 있어 보입니다.)
• 이제 남은 것은 이러한 discriminator를 가지고 어떻게 policy를 학습할 수 있느냐 입니다. 논문에서는 UVFA를 통해 USFA를 통해 얻은 적절한 feature를 학습하도록 하고,UVFA는 이전에 설명한 내용을 참조하시면 좋겠습니다.
  1. Adding Generalized Policy Improvement to VISR
     • General policy Improvement를 위해 어떻게 policies set을 구성하는지에 대해 알아보겠습니다. USFA \(\boldsymbol{\psi}(s,a,e(\pi))\)는 encoding function \(e(\pi) = \boldsymbol{w}\)를 통해 \(\boldsymbol{w}\)가 어떻게 나오느냐에 따라 maximize하려는 목표가 다르므로, GPI의 policies set은 결국 \(\boldsymbol{w}\)에 의한 set으로 정의됩니다. 가장 자연스러운 \(\boldsymbol{w}\)의 설정은 (2)에 의한 regression의 solution을 사용한 \(\boldsymbol{w}_{\mathrm{base}}\)를 하나 정한 뒤, Von Mises-Fisher distribution에 따라 \(\boldsymbol{w}\)를 sampling하는 것입니다. 이를 따라 (5)를 다시 나타내면 다음과 같습니다.
     \[Q^{\pi_0}(s,a)←\boldsymbol{\psi}(s,a,\boldsymbol{w}_{\mathrm{base}})^T\boldsymbol{w}_{\mathrm{base}}\] \[Q^{\pi_{1:k}}(s,a)←\boldsymbol{\psi}(s,a,\boldsymbol{w})^T\boldsymbol{w}_{\mathrm{base}}|\boldsymbol{w} \sim \mathrm{VMF}(\mu = \boldsymbol{w},\kappa)\] \[\pi(s) = \mathrm{argmax}_a\max_iQ^{\pi_i}(s,a)\]
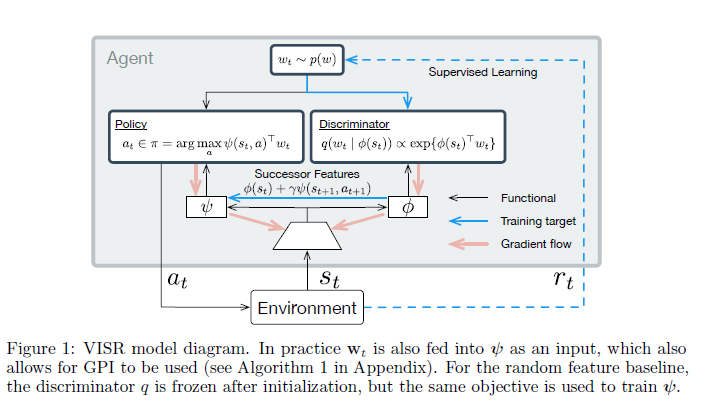
• Algorithm and model

  • 전 내용을 보시면 둘다 금방 이해하실 수 있습니다. \(\boldsymbol{\psi}\)는 USFA에서 자세하게 나와있지만, td-error를 통해 학습하고, \(\boldsymbol{\phi}\)는 nll loss를 통해 state를 잘 예측하도록 학습합니다.(결국 discriminator역할은 \(\phi\)를 통한 간접적인 posterior를 가지고 학습하게 됩니다.)

    

    

References

• Fast Task Inference with Variational Intrinsic Successor Features