읽기 전에, VISR과 APT를 읽고 오시길 바라겠습니다.

Abstract

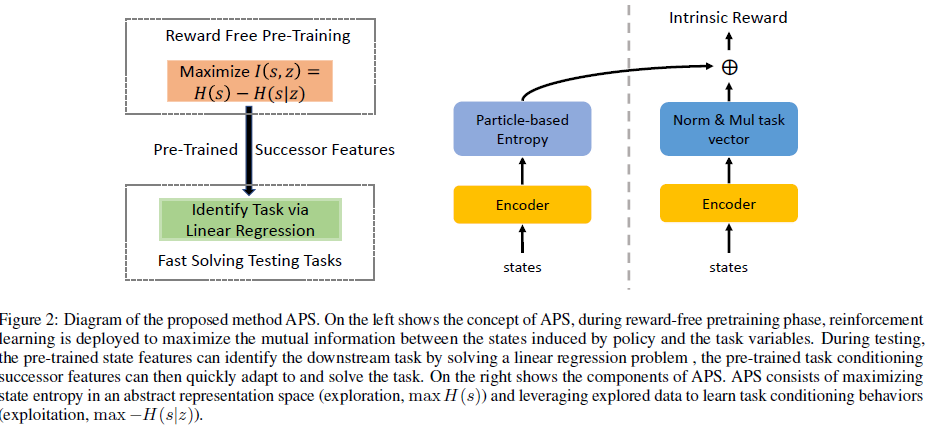
  • 이 논문도 역시 Mutual Information을 maximize하여 Unsupervised Pre-training을 진행하는데, VISR과 APT의 기법을 잘 섞어 단점들을 보완한 Algorithm, Active Pretraining With Successor Feature(APT) 를 소개합니다.

Introduction

  • 다른 computer vision, natural language processing 모두 pre-trained model을 통해 큰 진전을 이루었지만, RL은 아직도 scratch로부터 학습하는 것이 dominant합니다. 이는 RL algorithm이 새로운 task를 학습시킬 때 마다, scratch로부터 학습시켜야한다는 의미와 같은데, 이는 지능이 있는 생물의 특성과는 큰 대조를 이룹니다.
  • 이 차이를 메꾸기 위해 unsupervised pretraining RL이 최근 많이 연구되고 있고, 이는 environment의 reward 없이 pretraining을 시킨 상태에서, downstream task를 통해 extrinsic reward를 받으며 얼마나 잘 pretrain되었는지 data efficiency등을 확인하는 과정으로 이루어집니다.
  • SOTA unsupervised RL methods는 intrinsic reward를 이용하는 방법인데, 이는 extrinsic reward 없이 intrinsic reward만을 maximizing하여 의미있는 behavior를 만들어내는 방법입니다. 이는 VISR과 APT 두 가지 큰 흐름이 있는데, 이는 모두 장단점을 가지고 있습니다.

Preliminaries

  1. Successor Features

Method

  1. Variational Intrinsic Successor Features(VISR)
  2. Unsupervised Active Pretraining(APT)
  3. Empirical Evidence of the Limitations of Existing Models

aps

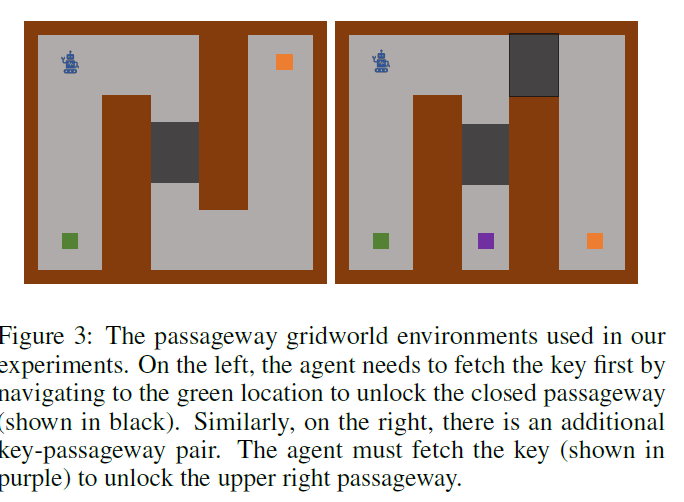
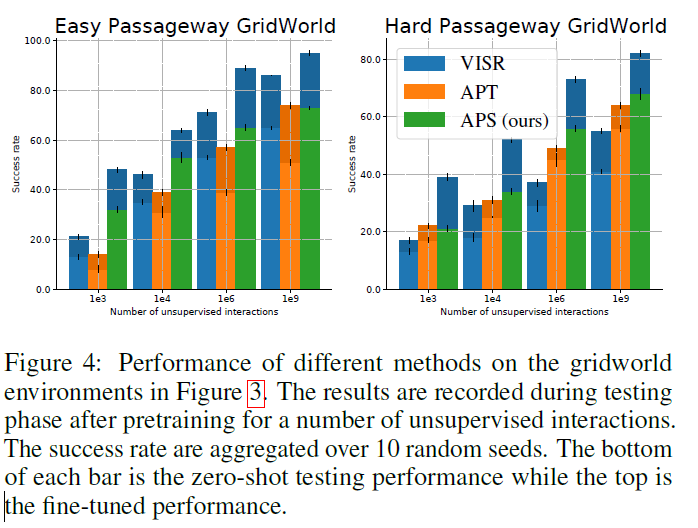
이 실험을 통해 VISR과 APT 두 방법의 한계를 보겠습니다. 이 실험은 좌측 상단의 로봇이 주황 지점까지 이동하는 실험입니다. 이 때, 초록색과 보라색을 누르면 막힌 길이 하나씩 열리게 됩니다. 좌측 실험은 우측 실험에 비해 열 길이 하나 적어 쉬운 task라고 할 수 있는데, 이 때 evaluation을 할 땐 초록색과 보라색의 key를 주우면 reward +1, 해결하면 +10을 주어서 테스트하였습니다. 이 실험에서 알 수 있는 점을 아래 figure를 보면서 확인하겠습니다.

aps

좌측 쉬운 task에 대해서는 VISR가 APT보다 좋은 성능을 보였지만, 어려운 task에 대해서는 APT가 VISR보다 좋은 성능을 보였습니다. 이는 VISR가 쉬운 task에서는 successor features를 downstream reward에 빠르게 적용할 수 있었다고 볼 수 있지만 어려운 task에서는 exploration이 잘 안되어 성능이 떨어졌다고 볼 수 있습니다.

  1. Active Pre-training with Successor Features

  • APT와 VISR 문제를 해결하기 위해 task variable z와 state에 대한 mutual information을 다음과 같이 나타냅니다.

    \[I(z;s) = H(s) - H(s|z)\]

    \(H(s)\)는 agent가 exploration하도록 돕고, \(-H(s|z)\) 는 task variable에 의한 agent의 trajectories가 불확실성이 낮도록 돕습니다.

  • 이 때 \(H(s)\)는 intractable하므로, APT에서 \(H(s)\)를 maximize하기 위해 주었던 reward를 그대로 사용합니다.

    \[r^{\mathrm{exploration}}_{\mathrm{APS}}(s,a,s') = \log(1+\frac{1}{k}\sum_{h^{(j)}\in N_k(h)}||h - h^{(j)}||^{n_h}_{n_h})\] \[\mathrm{where}\ h = f_{\theta}(s')\cdots (2)\]

  • \(H(s\vert z)\)는 VISR에서 \(H(z\vert s)\) minimizing할 때 썼던 variational approximation을 활용하는데, 이는 다음과 같습니다.

    \[F = -H(s|z) \geq \mathbb{E}_{s,z}[\log q(s|z)]\]

    증명은 VISR에도 있지만, 여기서도 증명을 해주었습니다. 간단히 KL-divergence의 성질을 이용합니다. 그리고 \(w\)를 \(z \equiv w\)로 restricting하면 VISR에서 사용한 같은 reward를 얻을 수 있습니다.

    \[r^{\mathrm{exploitation}}_{\mathrm{APS}} (s,a,s') = \log{q(s|w)} = \phi(s)^Tw \cdots(4)\]

    기존처럼, \(w\)와 \(\phi\)는 unit length를 지니고, \(q(s|w)\)는 scale parameter가 1인 Von Mises-Fisher distribution을 따르면 이 reward가 성립합니다. (이로 인해 VISR에서 자연스럽게 q의 VMF distribution에서 similar w 를 여러 개 뽑아 generalization하는 방법을 못써서 본문에서도 unit circle에서 뽑은 w를 하나 뽑아 쓰는 정도로 말합니다.)

    이 때, encoder \(f\)와 \(\phi\)의 weights를 공유하는 것이 학습에 도움이 됨을 보았는데, encoder는 Von-Mises distribution \(q(s|w)\)의 negative log likelihood를 minimizing하여 학습시킵니다. \(L = -\mathbb{E}_{s,w}[\log{q(s|w)}] = - \mathbb{E}_{s,w}[\phi(s_t)^Tw]\)

    (2)와 (4)의 Equation을 합쳐 reward를 쓰면 다음과 같습니다.

    \[r_\mathrm{APS}(s,a,s') = r^{\mathrm{exploitation}}_{\mathrm{APS}} (s,a,s') + r^{\mathrm{exploration}}_{\mathrm{APS}}(s,a,s')\] \[r_\mathrm{APS}(s,a,s') = \phi(s)^Tw +\log(1+\frac{1}{k}\sum_{h^{(j)}\in N_k(h)}||h - h^{(j)}||^{n_h}_{n_h})\] \[\mathrm{where}\ h = \phi(s')\]

    \(\phi\)의 output layer는 l2 normalization을 해야하고, 아까 언급했던 것 처럼 task vector \(w\)는 unit circle위의 uniform distribution위에서 뽑습니다.

Algorithm and resulting model**

aps 이 때, 본문에서는 representation learning에 대해 깊게 다루지 않아 \(f\)가 algorithm상에는 생략되었습니다. aps

References