Behavior From the Void: Unsupervised Active Pre-Training 논문 리뷰 및 설명

Abstract

• 이 논문은 reward-free environment에서 behavior과 representation을 배우는 algorithm, Active Pre-Training(APT)에 대해 소개합니다. 메인 아이디어로 비모수적인 방법을 통해 entropy를 maximize하여 environment를 탐색하는데, 이는 기존의 pixel-based environment에 대해 접근하기 어려웠던 density modeling를 하지 않음으로써 high-dimensional observation에 대해 explore할 수 있는 방법을 제시합니다.

Introduction

• Unsupervised pre-training은 computer vision, natural language modeling 모두 주목할만한 결과를 얻었습니다. 이는 본 task에서 data-efficient하게 학습될 수 있도록 만드는 것이 주 목적인데, 기존의 RL에선 count-based bonus등을 통해 새로운 state에 대해 reward를 주는 방식을 통해 exploration되도록 하였으나, 이는 high dimensional input space에서는 효과를 보이지 않음을 실험을 통해 보였습니다. 또한 ImiageNet을 pre-training했어도 real world robotics에는 전혀 도움이 되지 않았던 연구 결과 또한 존재합니다.
• 당연하게도 이러한 문제를 해결하기 위해선, task를 몰라도 스스로 environment를 탐색하고 새로운 state를 찾아내는 방법이 필요합니다. 이 논문은 기본적으로 entropy를 maximization하는 방법을 채택하였는데, 이는 사실 high dimensional state space에서는 oracle density를 구하기 어렵기 때문에 문제가 있었습니다. 하지만 비모수적 추정으로 state space를 어떤 representation space에 표현했을 때 samples 각자의 nearest neighbors에 대한 euclidiean distance의 평균을 구해 이를 maximize함으로써 모수에 대한 추정없이 탐색을 진행합니다.
• 이 접근법은 다양한 RL algorithm에 적용될 수 있는데, 이 논문은 DrQ라는 visual RL algorithm에서 SOTA를 보이는 algorithm에 적용되어 큰 data-efficiency의 개선을 보였습니다.
• 이 논문의 contribution은 다음 두 가지와 같이 요약될 수 있습니다.
  • Visual RL에서 Unsupervised pre-training의 새로운 방법을 제시함.
  • 다양한 downstream tasks에 대해 data efficiency를 개선함을 보임.

Related Work

1. Entropy Maximization
   • Entropy Maximization은 RL의 다양한 분야에서 쓰였는데 특히 inverse RL에서 많이 쓰였습니다. 다만 이런 적용에는 action space에서만의 entropy를 고려합니다.
   • State space entropy maximization은 최근에 exploration method에서 많이 쓰였는데, 이는 state space에 대한 density model을 추정하기가 어려워 확장성이 떨어졌습니다.
   • 최근 Mutti의 연구에서 particle based entropy를 maximize하는 것이 data efficiency를 높일 수 있는 것을 보였었는데, 이는 variance가 높을 뿐만 아니라, pixel input에 대해 어떻게 작동하는지 명확하게 설명하지 않습니다.
   • Badia의 연구에서 k-nearest neighbor based count bonus를 통해 exploration을 유도하는 방법에 대해 보였습니다. 그외에도 다양한 연구가 진행되었는데, count-based intrinsic reward에 의존하였다는 것이 이 연구와의 차이점입니다.
2. Data Efficiency in RL
   • model-based, contrastive learning등 다양한 방법이 data-efficiency를 높이기 위해 연구되었습니다. APT도 방법은 다르지만, data efficiency를 높이기 위한 방법으로, 함께 결합되면 더 큰 개선이 있을 수 있습니다.

Preliminaries

• Reinforcement Learning
• RL with Unsupervised Pre-Training

• 최근 unsupervised pre-training RL에서의 SOTA는 policy를 control하는 variable z와 state간의 mutual information을 maximizing하는 방식인데, 이를 수식으로 살펴보면 다음과 같습니다.

  \[\max{I(s;z)}= \max{H(z) - H(z|s)}\]

  z는 주로 fixed distribution으로, entropy를 최대화할 수 있는 uniform distribution을 사용합니다. 그리하여 이를 간소화하면 \(-H(z|s)\)를 maximize하는 식으로 볼 수 있는데, intractable하므로 여기서 variational lower bound를 사용해 \(q_\theta\)로 근사한 수식을 사용합니다. 정리하면 다음과 같습니다.

  \[J(\theta) = \sum_{s,z}p(s,z)\log{q_\theta}(z|s) = \mathbb{E}_{s,z}[\log{q_{\theta}(z|s)}]\]

  하지만 이 방법은 exploration이 부족합니다. mutual information을 위와 반대로 풀어 다음과 같은 mutual information을 maximize하는 방법도 존재합니다.

  \[\max{I(s;z)} =\max{H(s)} - H(s|z)\]

  이 방법도 variational approximation을 통해 다음과 같은 lower bound를 만들 수 있습니다.

  \[I(s;z) \geq\mathbb{E}_{s,z}[q_\theta(s|z)] - \mathbb{E}_s[\log{p(s)}]\]

  이 때, 마지막 term은 사전확률과 approximated 사후 확률이므로 다음과 같이 근사할 수 있습니다.

  \[\mathbb{E}_s[\log{p(s)}] \approx \mathbb{E}_{s,z}[\log{q(s|z)}]\]

  하지만 이도 비슷하게, exploration에서 한계를 보입니다. 그냥 state에 대한 entropy를 maximize하는 방식은 너무 burden해보입니다. 또한 이 방법들은 pixel input에 대해 어떻게 적용하는지 설명하지 않았습니다.

Unsupervised Active Pre-Training for RL

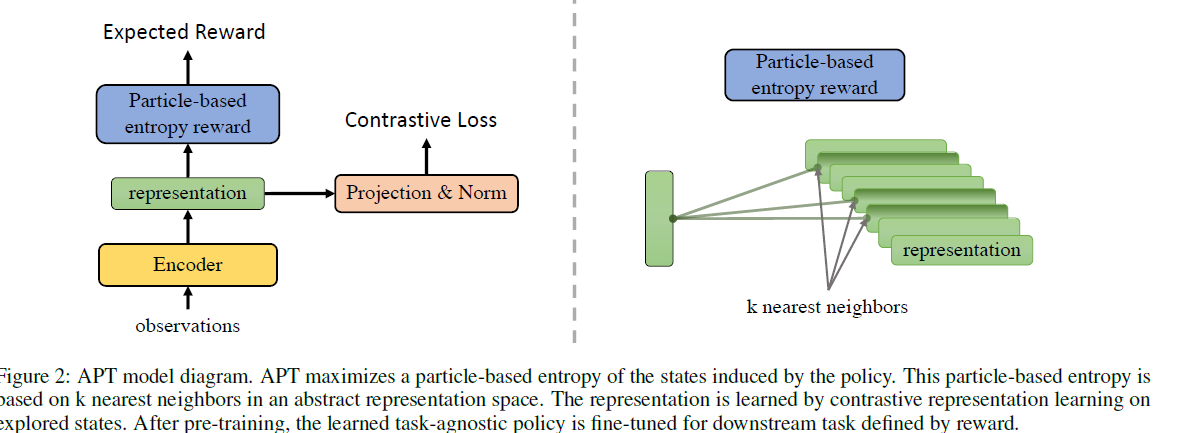
• 전체적인 학습은 state의 abstract representation space에서 entropy를 maximize하기 위해 reward \(r_t\)를 받도록 하는 과정을 보입니다. 이 때, pixel input은 low dimensional representation으로 mapping하는 function \(f_\theta : R^{n_s} → R^{n_z}\)도 contrastive learning을 통해 배우게 됩니다.
  1. Particle-based Entropy Maximization Reward
     • lower dimensional abstract representation space로 부터 entropy를 구하기 위해서 전에 설명했던 nonparametric particle-based entropy estimator를 사용하는데 이는 k개의 nearest neighbors에 기반해 entropy를 측정합니다.
     \[H_{\mathrm{APT}}(z) = - \frac{1}{n}\sum^n_{i=1}\log{\frac{k}{nv^k_i}} + b(k) \propto \sum^n_{i=1}\log{v^k_i} \cdots (7)\]

     \(b(k)\)는 k의 bias를 보정하기 위한 값, \(v^k_i\)은 단순히 \(z_i\)의 k neaest neighbors과의 거리를 반지름으로 하는 hyper-sphere의 volume입니다. 이는 생소해 보일 수 있지만, 기존의 KNN수식에 entropy로 다루기 위해 log를 씌운것과 bias correction term을 더한 것 외에 다른 점이 없습니다.(이 유도과정은 Singh(2003)의 연구를 참조하시면 됩니다.) 이 값은 다른 상수들을 제외하고 rough하게 마지막 term에 비례하게 되는데, Dobrushin (1958)의 연구에서 이 volume은 다음과 같이 표현함을 보입니다.

     \[v^k_i = \frac{||z_i - z^{(k)}_i||^{n_z}_{n_z}\cdot \pi^{n_z/2}}{\Gamma(n_z/2+1)} \cdots(8)\]

     이를 다시 (7)에 대입하면 entropy는 단순히 다음과 같이 나타낼 수 있음을 알 수 있습니다.

     \[H_k(z) \propto \sum^n_{i=1}\log{||z_i - z^{(k)}_i||^{n_z}_{n_z}}\]

     이 때, 실험적으로, 이를 평균으로 사용하고, 상수를 더하는 것이 stability를 위해 도움이 됨을 보였고 정리하면 다음과 같습니다.

     \[\hat{H}_{\mathrm{APT}}(z) = \log^n_{i=1}\log(c+\frac{1}{k}\sum_{z_i^{(j)}\in N_k(z_i)}||z_i - z_i^{(j)}||^{n_z}_{n_z})\]

     이를 통해 reward를 정의하면 다음과 같습니다.

     \[r(s,a,s') = \log(c+\frac{1}{k}\sum_{z_i^{(j)}\in N_k(z_i)}||z_i - z_i^{(j)}||^{n_z}_{n_z}) \\ \mathrm{where} \ z=f_\theta(s) \cdots (11)\]

     이때, next state \(s'\)가 particle로써 mapping function \(f\)에 의해 \(z\)로 변환되어 lower dimensional abstract representation으로 쓰입니다. (next state에 대해서 k-nearest neighbors를 구해 현 state에 reward를 주는 것이 타당합니다.) scale을 위해 reward는 running estimate of the mean으로 나누어 normalization하게 됩니다. 이 reward를 통해 자주 방문한 state는 nearest neighbors가 가까우므로 0로 감소함을 직관적으로 알 수 있습니다. 그리고 이를 바로 증명하는데, 간단하게 k보다 많은 아주 가까운 주변의 nearest neighbors를 방문하게되면, MDP는 stationary함을 가정하기 때문에, 무한히 states를 방문한다 했을 때, 이 distance가 0이 됨을 의미합니다. 이를 통해 (11)에서 정의했던 reward가 c=1로 뒀을 때, 0이 됨을 알 수 있습니다.

  • Learning Contrastive Representations
    • 이는 기존에 CURL이나 SPR등 RL에 적용되었던 contrastive learning이 성공적으로 의미있는 representation을 학습할 수 있음을 보았고 이는, 한 state와 다른 state간 잘 구별가능하도록 latent에 mapping된다는 것을 의미합니다.

    • replay buffer에서 sampling된 batch는 augmentation이 이루어지고, deterministic projection \(h_\phi(\cdot)\)에 의해 latent space \(z\)로 mapping됩니다. 이 때, 본 논문의 contrastive learning은 SimCLR과 똑같이 이루어집니다. N개의 data에 관하여 각각 다른 augmentation을 통해 만든 2개의 같은data에 대해 NCELoss를 적용하면 다음과 같은 수식이 나옵니다.

      \[\min_{\theta,\phi} - \mathbb{E} [\frac{\exp(h_\phi(f_\theta(s_i))^Th_\phi(f_\theta(s_j)))}{\sum^{2N}_{k=1}\mathbb{1}_{[k \neq i]}\exp(h_\phi(f_\theta(s_i))^Th_\phi(f_\theta(s_k)))}] \cdots(14)\]
    • data augmentation은 DrQ에서처럼, random shift와 color jitter기법을 사용합니다.
    • h는 SimCLR의 projection function \(g\)와 같이 fc로 구성됩니다.

    • algorithm과 architecture 모두 설명하였으니 쉽게 이해하실 것이라고 믿습니다. DrQ와 다른점에 대해 주황생 형광 표시가 되어있습니다.

      

      

References

• (Behavior From the Void: Unsupervised Active Pre-Training)[https://arxiv.org/abs/2103.04551]