Neural Combinatorial Optimization with Reinforcement Learning 논문 리뷰 및 설명

Neural Combinatorial Optimization with Reinforcement Learning

Abstract

• 이 논문은 Combinatorial Optimization problem에 Deep Reinforcement Learning을 적용한 논문입니다. Pointer Network와 Policy gradients를 결합해 TSP를 해결하는 모습을 보입니다.

Introduction

• Combinatorial Optimization(CO)은 computer science에서 근본적으로 다루어지고 있는 문제입니다. 이에 아주 기본적인 예로 Traveling salesman problem이 있는데, 간단하게 설명하자면, 모든 nodes를 총 edge weights가 최소가 되도록 방문하여 원래 node로 돌아오는 최적의 순서를 찾는 문제입니다. 이 때, 이 문제는 NP-hard로, 기존의 TSP solver는 휴리스틱한 탐색을 통해 이 경로를 찾고, 조금이라도 문제가 달라지면 처음부터 이를 다시 계산해야 했습니다. 반면에 ML method는 training동안 학습한 방법을 기반으로 이를 응용할 수 있기 때문에, 작업이 덜 들어갈 수 있습니다. 하지만 Supervised Learning method를 적용하는 것은 ground truth를 만드는 작업이 어려울 뿐더러, generalization에서 약한 모습을 보였습니다. 이 때 RL은 위의 두 가지 단점을 회피하는 매력적인 방법입니다.
• 이 논문은 CO에 DRL을 결합한 Neural Combinatorial Optimization(NCO)를 제안합니다. 이는 policy gradients를 기반으로 두 가지 학습 방법을 제시하는데, 첫 번째는 training set을 통해 학습을 진행한 후 test할 때는 policy를 fix하는 RL pretraining, 두 번째 pretraining없이 test에서 optimize를 진행하는 Active search입니다. 실전적으로 둘을 결합(RL pretraining-Active Search)한 것이 가장 좋은 성능을 냈습니다.

Previous Work

• TSP는 이미 많이 연구된 분야이고, 다양한 근사, 혹은 정확한 해를 도출하는 방법들이 제시되었습니다. 다만 위에서 언급한 문제와 같이 아직 해결하지 못한 문제들이 존재합니다.

Neural Network Architecture for TSP

• 이 논문은 2d euclidean TSP를 중심으로 서술합니다. 이는 n개의 도시에 대해 \(s = \{\boldsymbol{x}_i\}^n_{i=1},\ \boldsymbol{x}_i \in \mathbb{R}^2\) 로 나타낼 수 있고, 이 도시를 순회하며 가장 적은 edge weights의 순열을 찾는 policy \(\pi\)를 찾는 것이 목표입니다. 이 edge weights는 거리로 나타낼 수 있고, 총 거리에 대해 표현하면 다음과 같습니다.

  \(L(\pi |s) = \Vert \boldsymbol{x}_{\pi(n)} - \boldsymbol{x}_{\pi(1)} \Vert_2 + \sum^{n-1}_{i=1} \Vert \boldsymbol{x}_{\pi(i)} - \boldsymbol{x}_{\pi(i+1)}\Vert_2\) 이 때, 한 trajectory를 policy가 방문할 확률은 다음과 같이 표현 가능합니다.

  \[p(\pi \vert s) = \prod^n_{i=1} p(\pi(i) \vert \pi(<i),s)\]

  이는 기존의 sequence-to-sequence 문제로 해결할 수 있다는 것을 보이지만, 이런 접근 방식은 두 가지 단점을 지닙니다. 첫 째로, n개 이상의 도시에 대해 generalization할 수 없습니다. 둘째로 ground-truth를 가지고 학습을 시켜야합니다. 이러한 문제를 해결하기 위해 pointer network를 도입하여 첫번째 문제를 해결하고, RL을 도입하여 두번째 문제를 해결합니다.

1. Architecture Details
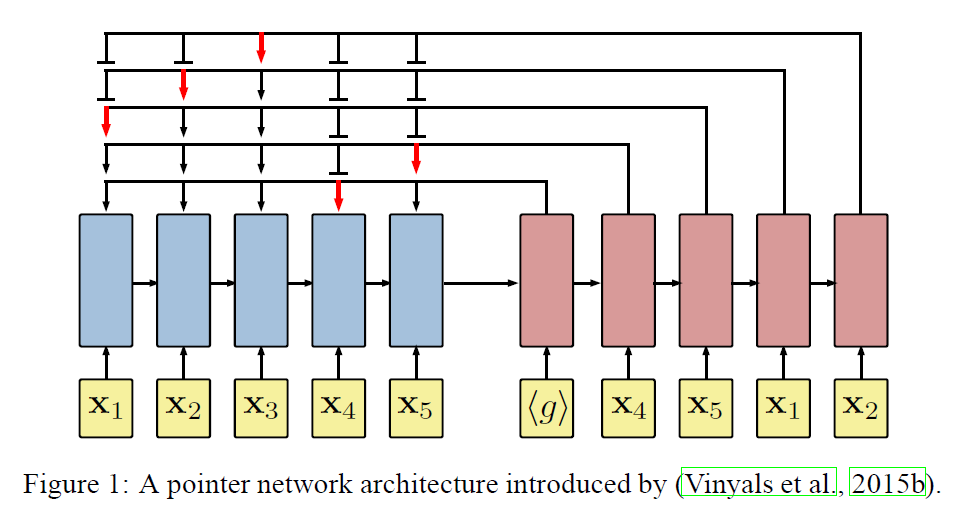
   • Pointer network는 encoder와 decoder로 이루어져 있습니다.

   

• encoder network는 recursive network를 통해 input sequence s를 순차적으로 받아, fixed length latent를 만듭니다. 이 때, input points는 embedding network를 통해 d-dimension으로 embedding된 상태입니다.
• decoder network는 recursive network를 가지고 attention network와 함께 다음 방문할 node에 대한 distribution을 생성합니다. 이때 선택된 다음 node는 다시 decoder의 input으로 들어가게 됩니다. decoder의 첫 node는 shape을 맞춘 trainable zero vector를 넣습니다.(그와 함께 encoder에서 나온 hidden state를 받아 recursive하게 사용합니다.)
• attention function을 설명하자면, query vector \(q = dec_i \in \mathbb{R}^d\)와 reference vectors \(ref= \{enc_1,...,enc_k\},\ \mathrm{where}\ enc_i \in \mathbb{R}^d\) 에 대해, \(A(ref,q)\)로 k 개의 reference에 대해 distribution을 내놓습니다. 이 distribution은 query \(q\)에 대해서 reference \(r_i\)에 pointing하는 정도를 나타냅니다. 이를 조금만 더 자세히 알아보자면 다음과 같습니다.
• Pointing mechanism

  • pointer network의 content based input attention section에 valid한 action만을 선택하기 위해 masking을 한 수식을 내놓습니다.

    \[u_i = \left\{\begin{matrix} v^T \cdot \tanh{W_{ref}\cdot r_i + W_q \cdot q} \ \mathrm{if} \ i \neq \pi(j) \ \mathrm{for \ all}\ j <i\\ - \infty \ \ \ \ \ \mathrm{otherwise \ \ \ for }\ \ i = 1,2,...,k \end{matrix}\right.\] \[A(ref,q;W_{ref},W_q,v) = softmax(u)\]

    decoder가 다음 방문할 node에 대한 distribution은 trainable weights를 생략하고 이렇게 나타낼 수 있습니다.

    \[p(\pi(j) \vert \pi(<j),s) = A(enc_{1:n},dec_j)\]
  • 또한 이전에 연구되었던 glimpses에 대해 설명하는데, 이도 appendix에서 살펴보면 다음과 같습니다.
  • Attending mechanism

    • glimpse function \(G(ref,q)\)에 대해 attention function과 같은 input을 받고 같은 연산을 취합니다. 하지만 마지막에 reference vector에 의한 weight를 받은 linear combination연산이 추가되는데, 이는 query에 대해 모든 reference의 가중치를받은 \(g\)를 이용해 query를 대체하게 됩니다.

      \[p = A(ref,q;W^g_{ref},W^g_q,v^tg)\] \[G(ref,q;W^g_{ref},W^g_q,v^g) = \sum^k_{i=1}r_ip_i\]

Optimization with Policy gradients

• pointer network의 parameter를 \(\boldsymbol{\theta}\)로 나타냈을 때, 학습 objective는 다음과 같이 나타낼 수 있습니다.

  \[J(\boldsymbol{\theta}|s) = \mathbb{E}_{\pi \sim p_\theta(\cdot|s)}L(\pi \vert s)\]

• Policy gradient method중 baseline을 사용한 REINFORCE algorithm을 사용하는데 이는 다음과 같습니다.

  \[\nabla_\theta J(\theta \vert s) = \mathbb{E}_{\pi \sim p_\theta(\cdot \vert s)} [ (L(\pi \vert s) - b(s)) \nabla_\theta \log{p_\theta(\pi \vert s )}]\]

  graphs에 대해 \(\mathcal{S}\)에서 i.i.d하게 뽑아 한번의 episode를 \(\pi \sim p_\theta(\cdot \vert s_i)\) 같이 표현할 때, 이는 Monte Carlo sampling으로 볼 수 있고, 이를 다음과 같이 근사할 수 있습니다.

  \[\nabla_\theta J(\theta \vert s) \approx \frac{1}{B}\sum^B_{i=1}[ (L(\pi_i \vert s_i) - b(s_i)) \nabla_\theta \log{p_\theta(\pi _i\vert s_i)}]\]

  baseline을 선택하는 가장 간단한 방법은 reward의 exponential moving average를 사용하는 방법이고 기존 알고리즘에서도 충분함을 보였으나, 이는 꽤 복잡한 graph \(s\)에 대해 optimial path에 대한 length가 baseline을 넘어버리면 optimal policy라도 adventage가 음수가 되는 문제가 발생합니다. 그렇기에 critic network를 도입하여 \(b\)를 대체합니다. critic은 다음과 같이 실제 length와의 l2 loss를 활용해 학습합니다.

  \[\mathcal{L}(\theta_v) = \frac{1}{B} \sum^B_{i=1} \Vert b_{\theta_v}(s_i) - L(\pi_i \vert s_i) \Vert^2_2\]

• Critic’s Architecture for TSP

  • input sequence로부터, baseline prediction \(b_{\theta_v}(s)\)를 어떻게 mapping하는지에 설명합니다. 이는 Pointer Network의 encoding과 glimpsing 후 fc를 거치는 방법으로, 좀더 자세히 1)LSTM encoder와 2)LSTM process block, 3)2-layer ReLU fc로 이루어 있습니다. 첫 째로, encoder는 input sequence를 latent memory state와 hidden state h로 만듭니다. 두 번째로 process block은 P steps동안 hidden state에 대해 memory state를 이용해 glimpsing을 하는데 이는 chapter 5에서 설명한 대로 이루어집니다. 마지막으로 fc를 거쳐 scalar 값을 얻습니다.

  • training은 A3C처럼 이루어질 수 있습니다. 이 때 workers는 mini-batch를 통해 gradients를 구합니다. 이를 통해 algorithm 1을 먼저 보겠습니다. 일반적인 A2C와 같이 나타내었습니다.

    

1. Search Strategies
   • 이 때, 한 episode에 대해 length를 계산하는 비용이 비싸지 않으므로, TSP agent는 한 graph에서 여러번 simulation을 하여 최고의 episode를 골라낼 수 있습니다. 이 특성을 이용한 두가지 전략을 소개합니다.
   • Sampling
   • policy를 이용해 다양한 candidates를 만들어 가장 최적의 것을 고르는 방법입니다. 이 때 기존 휴리스틱한 solvers처럼 제약을 두는건 아니지만 sampling할 때 temporature를 통해 diversity를 조절할 수 있습니다. 이는 decoding에 적용되었을 때, 큰 진전을 보였습니다. - Active Search

   • 하나의 graph로부터 test를 할 때, agent의 network를 fix하거나 reward function을 무시하지 않고, 계속 학습하는 방법입니다. 이는 이미 학습된 모델을 사용할 때 효과적이나(RL pretraining-Active search), 학습시키지 않은 상태에서 바로 사용해도(Active Search) 잘 작동함을 보였습니다. Active search는 기존에 보인 Algorithm 1 에서도 적용할 수 있으나, 하나의 graph로만 input을 제한해야합니다. 이 때 이 방법은 하나의 graph만 사용하므로 기존의 exponential moving average baseline을 사용할 수 있는데 이를 Algorithm 2에서 나타냅니다. 마지막으로 nodes는 random하게 shuffle하여 input에 들어갔을 때, sampling단계에서의 stochasticity를 높여 성능이 좋음을 보았습니다.

     

References

• Neural Combinatorial Optimization with Reinforcement Learning