Attention, Learn to Solve Routing Problems! 논문 리뷰 및 설명

Attention, Learn to Solve Routing Problems!

Abstract

• 최근 Combinatorial Optimization Problems을 해결하는 방법을 배우는 아이디어는 개발 비용을 줄일 수 있기 때문에 유망한 분야 중 하나입니다. 이를 실제로 구현해서 사용하기 위해선 좀더 좋은 모델과 학습방법이 필요한데 이 논문에서는 그 두가지를 모두 제시합니다.
  • 첫 째로, Pointer Network보다 장점이 많은 attention 기반의 모델을 제시합니다.
  • 둘 째로, REINFORCE에서 critic없는 baseline을 제시하여 학습을 단순화 합니다.

  이러한 방법은 VRP, OP, PCTSP등에서 많은 baseline보다 좋은 성능을 보입니다.

Introduction

Related Work

• 대부분 이전에 리뷰한 내용이므로 생략합니다.

Attention Model

• Attention model을 TSP에서 쓰기 위해 기존의 model과 달라진 점에 대해(input, mask, decoder context) 설명해야합니다. 이를 표현하기 위해 notation부터 살펴보면, 각 TSP의 한 graph를 \(s\)로 표현하고, 그안의 각 \(n\)개의 nodes에 대한 feature를 \(\boldsymbol{x}_i\)로 나타냅니다.

• 모든 순열에 대한 solutions \(\boldsymbol{\pi} = (\pi_1,...,\pi_n)\)에 대해 stochastic policy \(p(\boldsymbol{\pi} \vert s )\)는 \(\boldsymbol{\theta}\)에 의해 parameterize된다면 다음과 같이 나타낼 수 있습니다.

  \[p_\theta(\boldsymbol{\pi} \vert s ) = \prod^n_{t=1} p_{\boldsymbol{\theta}}(\pi_t \vert s , \boldsymbol{\pi}_{1 :t-1}) \cdots(1)\]

  encoder는 모든 input node를 weight sharing하여 embedding하고, decoder는 (1)의 우측 항의 연산을 \(\boldsymbol{\pi}\)에 의해 sequential하게 내놓는 역할을 합니다. 이 때, TSP는 처음 node로 들어가야하고, 현재 방문한 node에 대한 정보를 가지고 있어야하므로, 이 두 정보가 context node(vector)와 함께 decoder에 들어가게 됩니다.

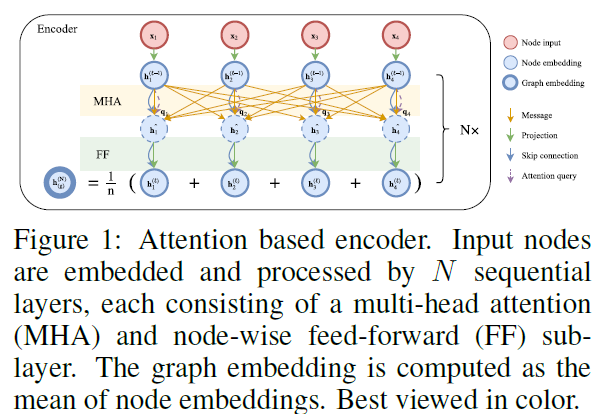
1. Encoder

• encoder는 transformer의 architecture에서 positional encoding을 뺀 형태입니다. 이 때 처음 input은(2-d TSP에선 \(d_x = 2\)) linear projection을 통해 \(d_h\) dimension으로 embedding 됩니다. 이 때 사용되는 weight와 bias를 \(W^x, \boldsymbol{b}^x\)로 표현하면 다음과 같습니다.

  \[\boldsymbol{h}^{(0)}_i = W^x \boldsymbol{x}_i + \boldsymbol{b}^x\]

  이 후 N개의 multi-head attention layer를 거치게 되는데 이를 통해 나온 각 노드 \(\boldsymbol{h}^{N}_i\)에 대해 mean을 취한 \(\bar{\boldsymbol{h}}^{N}_i\)와 함께 decoder에 들어가게 됩니다.

• Attention layer

  • 이는 이전에 Learning Heuristics for the TSP by Policy Gradient를 설명할 때 설명했으므로(MHA랑 FF만을 설명했는데, batch normalization과 skip connection을 더한 수식은 다음과 같습니다.)

    \[\hat{\boldsymbol{h}}_i = \mathrm{BN}({\boldsymbol{h}}_i^{(l-1)} + \mathrm{MHA}^l_i({\boldsymbol{h}}^{(l-1)}_i,...,{\boldsymbol{h}}^{(l-1)}_n))\] \[{\boldsymbol{h}}^{(l)}_i = \mathrm{BN}({\hat{\boldsymbol{h}}}_i^{(l-1)} + \mathrm{FF}^l(\hat{\boldsymbol{h}}_i)\]

2. Decoder

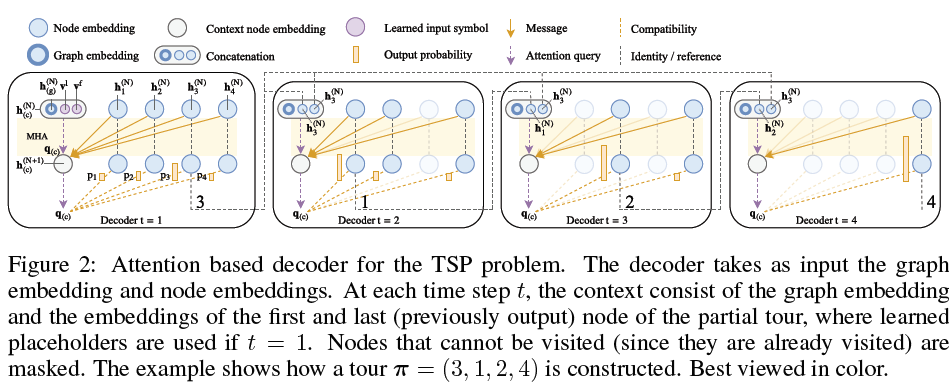
• decoder는 encoder에 의한 embedding과 이전 자신의 output을 통해(embedding된) output을 내놓습니다. 이때 decoding context를 나타내기 위해 context node를 사용하는데 이 방법은 뒤에서 설명합니다. 먼저 그림으로 나타내면 다음과 같습니다.

  

• Context embedding

  • 시점 t에서 decoder의 context는 encoder와 t까지의 output에 의해 나타냅니다. 이를 수식으로 나타내면, 이전에 언급했듯, 마지막 output node와 첫 node를 같이 넣어 context를 만듭니다.

    \[\boldsymbol{h}^{(N)}_{(c)} = \left\{\begin{matrix} [\bar{\boldsymbol{h}}^{(N)},\boldsymbol{h}^{(N)}_{\pi_{t-1}},\boldsymbol{h}^{(N)}_{\pi_1}] \ \ t>1\\ [\bar{\boldsymbol{h}}^{(N)},\boldsymbol{v}^1,\boldsymbol{v}^f] \ \ \ \ \ \ \ \ \ t=1\end{matrix} \right.\]

    \(\boldsymbol{h}^{(N)}_{(c)}\)는 \((3 \cdot d_h)\mathrm{-dimensional}\) vector입니다. 이는 다시 encoder로부터 나왔던 embedding \(h^{(N)}_i\)와 함께 multi-head attention을 진행합니다. 이를 나타내면 다음과 같습니다. (\(\boldsymbol{h}^{(N)}_{(c)}\)는 \(W^Q\)에 의해 다시 dimension을 맞춥니다.)

    \[\boldsymbol{q}_{(c)} = W^Q\boldsymbol{h}_{(c)}, \ \boldsymbol{k}_i = W^K\boldsymbol{h}_i, \boldsymbol{v}_i = W^V \boldsymbol{h}_i\]

    이를 통해 모든 노드의 query/key, \(u_{(c)j}\)에 대해 다음과 같이 나타낼 수 있습니다.

    \[u_{(c)j} = \left\{\begin{matrix} \frac{\boldsymbol{q}^T_{(c)} \boldsymbol{k}_j}{\sqrt{d_k}}\ \mathrm{if} \ \ j \neq\pi_{t'} \ \ \forall t' < t\\ -\infty \ \ \ \mathrm{otherwise}\end{matrix} \right.\]

    이를 softmax하여 \(\boldsymbol{v}_i\)와 곱합니다. 이 때 M개의 head로 나눠 연산합니다. 이를 통해 나온 head에 대해 각 weight를 곱해 multi-head attention을 구합니다.

    \[\boldsymbol{h}'_{(c)} = \sum_ja_{(c)j}\boldsymbol{v}_j ,\ a_{(c)j} = \frac{e^{u_{(c)j}}}{\sum_{j'}e^{u_{(c)j}}}\] \[MHA_{(c)}(\boldsymbol{h}_1,...,\boldsymbol{h}_n)= \sum^M_{m=1}W^O_m\boldsymbol{h}'_{(c)m}\]

    이는 encoder의 연산과 유사한데, skip-connection, batch norm, feed-forward를 사용하지 않습니다. 이런 연산을 보면, \(\boldsymbol{h}^{(N+1)}_{(c)}\)는 glimpse와 유사함을 알 수 있습니다.

• Calculation of log-probabilities

  • decoder의 마지막 layer는 \(p_{\boldsymbol{\theta}}(\pi \vert s, \boldsymbol{\pi}_{1:t-1})\)를 구하기 위해 single attention head를 통한 attention을 진행합니다. 이 때 기존의 NCO에서 사용한 clipping을 사용합니다.

    \[u_{(c)j} = \left\{\begin{matrix} C \cdot \frac{\boldsymbol{q}^T_{(c)} \boldsymbol{k}_j}{\sqrt{d_k}}\ \mathrm{if} \ \ j \neq\pi_{t'} \ \ \forall t' < t\\ -\infty \ \ \ \mathrm{otherwise}\end{matrix} \right.\]

    이를 softmax를 통해 probability처럼 사용합니다.

    \[p_i = p_{\boldsymbol{\theta}}(\pi_t = i \vert s, \boldsymbol{\pi}_{1:t-1})= \frac{e^{u_{(c)i}}}{\sum_je^{u_{(c)i}}}\]

1. Reinforce with greedy rollout baseline
   • 기존의 REINFORCE를 진행하나 이 때, baseline을 구하는데 있어, exponential moving average나 critic을 통해 구하지 않습니다. 이를 아래에서 설명합니다.

\[\nabla \mathcal{L}(\boldsymbol{\theta} \vert s ) = \mathbb{E}_{p_\theta(\boldsymbol{\pi} \vert s)}[(L(\boldsymbol{\pi}) - b(s)) \nabla \log{p_{\boldsymbol{\theta}}(\boldsymbol{\pi} \vert s)]}\]

• Motivation
• Determining the baseline policy
  • baseline으로 DQN에서 target Q network정하던 것처럼 fixed policy \(p_{\boldsymbol{\theta}^{\mathrm{BL}}}\)를 정하는데, 이는 t-test를 통해 기존보다 향상됨이 검증된 policy를 사용합니다.
• Analysis

• Algorithm

  

  baseline을 구하는 방법을 제외하곤 기존 REINFORCE algorithm과 같습니다.

• Efficiency

References

• Attention, Learn to Solve Routing Problems!