Dream to Control: Learning Behaviors by Latent Imagination

Abstract

  • Neural network를 이용해 High-dimensional input에 대한 world model을 배우는 것은 agent의 behavior를 학습시키는데 있어 다양한 방향으로 도움을 줄 수 있습니다. 본 논문은 Dreamer라는 latent imagination을 통해 long-horizon tasks를 해결하는 algorithm을 제시합니다.

Introduction

  • Parametric world model은 world에 대한 knowledge를 agent에게 학습시킬 수 있는 방법을 제공합니다. 이러한 parametric model의 latent dynamics model은 Representation model, Transition model, Reward model로 구성되며, high-dimensional input을 compact state space로 변환하는데, 이는 environment와 interaction없이 parallel하게 학습할 수 있도록 합니다. 이 때, policy는 이 dynamics model과 함께, 다양한 방법으로 학습이 가능한데, 이러한 정해진 길이의 imagination을 하는 것은 shortsighted optimization하려하는 경향을 보이는 단점이 있습니다. Dreamer는 이를 뒤에서 좀 더 자세히 설명할 exponentially weighted value function을 통해 해결합니다.

  • 본 논문의 contribution은 다음과 같습니다.

    • Learning long-horizon behaviors by latent imagination

      • policy의 action에 대해서 gradient를 analytic하도록(gradients가 끊기지 않고 chain rule을 통해 update할 수 있다는 정도로만 이해하셔도 좋을 것 같습니다.) reparameterization trick을 사용합니다.

    • Empirical performance for visual control

      • Data-efficiency, computation time, final performance모두 DeepMind Control Suite benchmark에서 준수한 성능을 보였습니다.

Control with World Models

  • Reinforcement learning

    • visual control problem을 Partially observable Markov decision process로 정의합니다.

      • time step \(t \in [1;T]\)

      • continuous vector-based actions \(a_t \sim p(a_t \vert o_{\leq t, a < t})\)

      • high-dimensional observations, scalar rewards \(o_t,r_t \sim p(o_t,r_t \vert o_{<t},a_{<t})\)

      • maximize expected sum of rewards \(E_p(\sum^T_{t=1}r_t)\)

    • Agent components

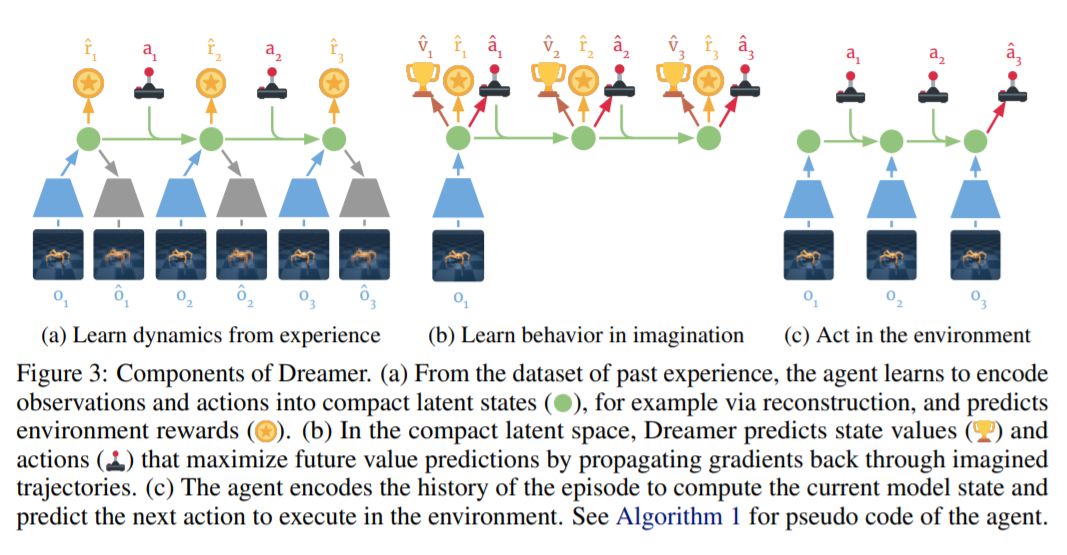
      • agent는 imagination을 통해 학습할 때 주로 dynamics를 학습하는 부분과, policy를 학습하는 부분, 그리고 environment와 interaction하는 세 가지로 나타낼 수 있습니다. 이를 천천히 설명하도록 하겠습니다.

    • Latent Dynamics(Dynamics를 학습하는 부분에 대한 설명)

      • Dreamer의 dynamics model은 또 세 가지 파트로 나뉘어집니다. high-dimensional input을 compact state로 mapping해주는 representation model, 이 후 compact state로 부터 transition probability를 approximate하는 transition model, reward model이 있습니다. 이를 나타내면 다음과 같습니다.
      \[\mathrm{Representation \ model } : \ p(s_t \vert s_{t-1},a_{t-1},o_t)\] \[\mathrm{Transition \ model} : q(s_t \vert s_{t-1},a_{t-1})\] \[\mathrm{Reward \ model} : \ q(r_t \vert s_t)\]

      여기서 혼동하지 말아야 할 것은, 실제 environment로부터 받는 observation에 대해 \(o_t\)로 표현하고, model이 만드는 compact state에대해 \(s_{t+1}\)로 표현하게 됩니다. 뒤의 Learning latent dynamics에서 좀 더 깊게 설명하겠습니다.

Learning Behaviors by Latent Imagination

dreamer

  • Imiagination environment

    • latent dynamics는 Markov decision process로 정의합니다. 이는 compact state \(s_t\)가 markovian하므로 reasonable합니다. imagination에 대한 time index는 \(\tau\)로 표현합니다.

  • Action and value models

    • Action model : \(a_\tau \sim q_\phi(a_\tau \vert s_\tau)\)

    • Value model : \(v_\psi(s_\tau) \approx \mathbb{E}_{q(\cdot \vert s_\tau)}(\sum^{t+H}_{\tau = t} \gamma^{\tau-t}r_\tau)\)

    • 중요한 점은 action model(policy)가 tanh-transformed Gaussian을 통해 reparameterized sampling을 가능하게 해서 gradients가 analytic하다는 점입니다.

      \[a_\tau = \tanh(\mu_\phi(s_\tau)+\sigma_\phi(s_\tau)\epsilon),\ \ \epsilon \sim \mathrm{Normal}(0,\mathbb{I})\]

  • Value estimation

    • 세 가지 value estimation을 제시하고, dreamer에선 어떤 value estimation을 사용하는지 보입니다.

      • \(V_R(s_\tau) = \mathbb{E}_{q_\theta,q_\phi}(\sum^{t+H}_{n=\tau}r_n)\) 는 value moded 없이 horizon까지의 imagined reward expectation을 사용합니다. 이는 n-step이후의 reward를 무시하게 되므로 초반에 말한 shortsighted될 가능성이 있습니다.

      • \(V^k_N(s_\tau) = \mathbb{E}_{q_\theta,q_\phi}(\sum^{h-1}_{n=\tau}\gamma^{n-\tau}r_n + \gamma^{h-\tau}v_\psi(s_h))\)는 horizion까지의 reward와 value model에 의한 estimation을 가지고 value estimation을 구성합니다.

      • \(V_\lambda(s_\tau) = (1-\lambda)\sum^{H-1}_{n=1}\lambda^{n-1}V^n_N(s_\tau) + \lambda^{H-1}V^H_N(s_\tau)\) 표기가 애매하지만 value model이 H개로 보는게 아닌, 하나의 value model에 대해 exponentially weighted average를 구하면 됩니다. 실전적으로 GAE에서 사용한 value estimation과 같이 구합니다.

  • learning objective

    • Action model의 objective는 \(\max_\phi \mathbb{E}_{q_\theta, q_\phi}(\sum^{t+H}_{\tau=t}V_\lambda(s_\tau))\), value model의 objective는 \(\min_\psi\mathbb{E}_{q_\theta,q_\phi}(\sum^{t+H}_{\tau=t}\frac{1}{2}\Vert v_\psi(s_\tau) - V_\lambda(s_\tau)\Vert)\)로, action이 discrete할 때, straight-through gradients를 통해 gradients를 analytic하게 유지합니다.

Learning Latent Dynamics

  • Reconstruction

    • PlaNet의 RSSM model과 같은 architecturing을 하였습니다. 이는 deterministic part와 stochastic part로 나뉘어, Recursive layer로 어떤 distribution의 deterministic한 properties를 만들어 stochastic한 state space로의 mapping을 유도합니다. 그리고 dynamics는 다음과 같은 Loss function을 가집니다.

      \[\mathcal{J}_\mathrm{REC}= \mathbb{E}_p(\sum_t(\mathcal{J}^t_o+\mathcal{J}^t_R+\mathcal{J}^t_D))+\mathrm{const},\] \[\mathcal{J}^t_O=\ln q(o_t \vert s_t),\] \[\mathcal{J}^t_R = \ln q(r_t \vert s_t),\] \[\mathcal{J}^t_D = -\beta \mathrm{KL}(p(s_t \vert s_{t-1},a_{t-1},o_t) \Vert q(s_t \vert s_{t-1}, a_{t-1}))\]

      이를 유도하는 식은 appendix의 VIB로도 가능하고, PlaNet에서의 loss function의 결과와 결국 동일합니다. 개인적으로 appendix의 수식이 조금 틀리고(summation의 남용) distribution에 대해 엄밀하게 어떻게 같은 distribution인가에 대해 고민하게 만들어서 깊게 보진않았습니다. 하지만 본질적으로 dataset에서의 observation에서의 정보량은 제한하면서 만들어낸 observation에 대해 mutual inforamation을 maximize하겠다는 의미입니다. 이전에 PlaNet에서의 설명을 통해 설명했지만 model들은 gaussian distribution을 가지므로 간단하게 MLE를 maximize하기 위해 observation model과 reward model의 l2 loss를 구하게되고, representation model과 transition model의 분포를 맞추기 위해 KL divergence로 이루어진다는 것을 명료하게 알 수 있습니다.

  • Contrastive estimation

    dreamer

References