Deep Reinforcement Learning and Deadly Triad
Abstract
- Temporal difference learning에 있어서 문제를 야기할 수 있는 deadly triad를 조금 더 실험적으로 분석한 논문입니다. 이 deadly triad는 function approximation, bootstrapping, off-policy learning으로 구성되어 있습니다. 그리고 이 세가지가 한 training에 결합되었을 때, value estimation이 diverge할 수 있는 문제를 DQN을 통해 실험적으로 어떤 요소가 얼만큼 영향을 미치는지 보입니다.
Introduction
- Off-policy learning method는 많은 분야에서 SOTA를 보이며 자주 쓰이는 방법이나, 여전히 이론적으로 이를 괴롭히는 문제들에 대해 직면하고 있습니다. 이는 policy가 diverge할 수 있는 가능성을 내포하고 있는데, 이러한 우려와는 다르게 많은 off-policy learning methods가 뛰어난 성능을 보이고 있습니다. 본 논문을 통해 이러한 현상을 이해하고, 해결할 방법에 대해 생각해 볼 수 있습니다.
The Deadly Triad in Deep Reinforcement Learning
-
먼저, 이 Triad를 이루는 세가지 요소를 먼저 조금만 더 살펴보겠습니다.
-
Bootstrapping
- 이는 한 time step에서의 value estimation을 update하기 위해 이후의 time step에 대한 value estimation을 이용하는 것을 의미합니다. 이때, vanilla DQN은 1 step을 사용하지만, n step 동안 실제로 받는 reward와 n step이후에 대한 value estimation을 통해 bootstrapping에 대한 영향을 줄일 수 있습니다.
-
Function approximation
- environment 전체를 탐색할 수 없으므로, state에 대한 generalization이 필요합니다. 이 때, 최근엔 function approximation을 위해 Neural Net을 사용하는데, 이 NN의 size를 바꿔가며 function capacity이 성능에 어떤 영향을 끼치는지에 대한 실험을 진행합니다.
-
Off-Policy
- DQN과 같은 off policy를 쓰는 것 외에도 TD error에 따른 prioritization을 주는 PER의 테크닉을 실험합니다.
-
Building Intuition
-
TD learning을 통해 update할 value function \(v\)에 대한 weights \(\boldsymbol{w}\)는 실제 policy \(\pi\)에 대한 optimal value \(v_\pi\)와 같아지도록 학습이 되어야 합니다. 이를 위해 update할 weights는 다음에 비례합니다.
\[\Delta \boldsymbol{w} \propto (R_{t+1}+\gamma v_{\boldsymbol{w}}(S_{t+1})-v_{\boldsymbol{w}}(S_t))\nabla_{\boldsymbol{w}}v_{\boldsymbol{w}}(S_t) \cdots(1)\]이 때, \(v_{\boldsymbol{w}}(S_{t+1})\)은 아직 가보지 않은 다음 time step에 대한 estimation인데, 이 때, 실험적으로 edge case를 만들어 triad에 대한 diverging을 확인할 수 있습니다. 이 예제는 Tsitsiklis와 Van Roy의 연구에서 등장합니다.
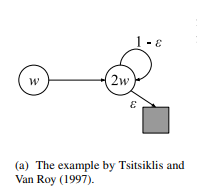
다음과 같은 상황에 대해 생각해 보겠습니다. 각 state에 대한 feature 는 single scalar feature \(\phi\)를 이용해 \(\phi(s_1) =1, \phi(s_2) = 2\)로 정의합니다. 그리고, estimated value는 각각 update할 weight에 대해 scalar feature를 곱한 \(v(s) = w \times \phi\)로 정의합니다. 그러므로 각 state에 대한 estimated value는 \(v(s_1) = w, v(s_2) =2w\)로 정의할 수 있습니다. 그리고, 모든 상황에서 받게되는 reward는 zero로 정의합니다. 그렇다면, 결국 weights를 iterative하게 update하여 \(v(s)\)에 대해 zero를 만들어주기 위해 \(w\)는 zero가 되는 것이 optimal입니다. on-policy를 통하여 update하게 되었을 때는, 전혀 문제가 발생하지 않습니다. 하지만 이 때, off-policy update를 통해 계속해서 \(s_1\)에 대한 value만을 update하는 상황에 대해 생각해보겠습니다. 그렇다면 (1)에서 처럼 value의 update양을 정해주게 되면, \(w ≠0, \gamma >\frac{1}{2}\)인 상황에 대해서 diverge하게 됩니다. 이는 on policy처럼 \(w\)를 update해주지 않으면 어떤 비율로 \(v(s_1)\)를 update하든 충분히 큰 \(\gamma\)에 대해 diverge합니다. 하지만 이 때, \(\phi\)에 0이 아닌 어떤 trainable 상수를 더해주면 결국 converge합니다. weights가 상수값만큼 더 update되므로 당연합니다. 하지만 이런식으로 우리는 어떤 방식에 의해 문제가 발생하는지 예에 대해 이해할 수 있었습니다.
Hypotheses
-
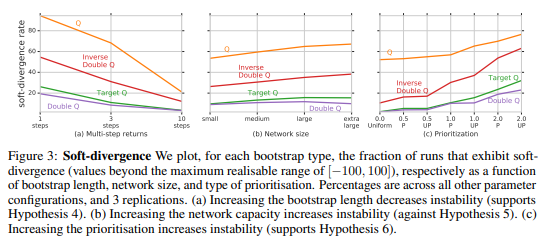
algorithm을 이루는 다양한 요소를 나누어서 각각 얼마나 divergence에 기여하는지에 대해 실험합니다. 그러기 위해 본 논문에서는 여섯가지 가설을 제시합니다.
-
Q-learning과 neural network의 결합만으로도 divergence할 확률이 줄어든다.
-
Target network를 사용해 bootstrapping함으로써 divergence할 확률이 줄어든다.
-
Overestimation을 막을수록 divergence할 확률이 줄어든다.
-
긴 Multi-step learning을 할수록 divergence할 확률이 줄어든다.
-
Network 크기가 클수록 divergence할 확률이 줄어든다.
-
Update에 대한 prioritization을 많이 할수록 divergence할 확률이 는다.
-
-
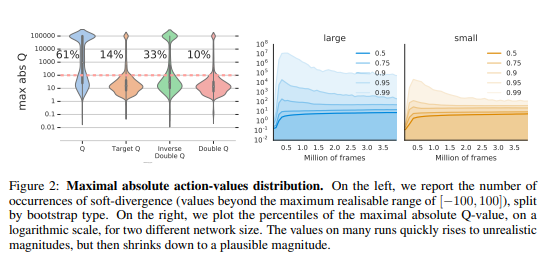
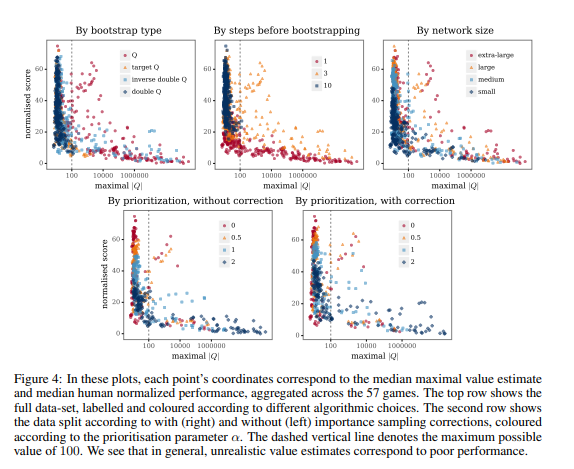
이후엔 실험적인 것으로 크게 설명할 것은 없습니다. 하지만 Overestimation이 왜 발생하는지에 대해 조금만 더 설명하겠습니다. 이는 learning중, function approximation을 사용하기 때문에, 비슷한 state에 대해 비슷한 estimated value가 나오기 때문에 발생합니다. 결국 이는 current state에 대해 update를 하였다고 해도 next state와 current state가 비슷하다면 둘 모두 estimated value가 오르기 때문에 계속해서 state에 대한 estimated value가 증가합니다. 본 논문에서는 이렇게 비현실적으로 높아진 estimated value에대해 soft divergence라고 부릅니다.