Learning Latent Dynamics for Planning from Pixels 논문 리뷰 및 설명

Learning Latent Dynamics for Planning from Pixels

Abstract

• Planning은 environment의 dynamics를 아는 상태의 control task를 해결하는 좋은 접근법으로 알려져 있습니다. 그러나 unknown environment로 부터 정확한 dynamics를 agent가 배우는 것은 아직까지도 큰 문제로 남아있습니다. 논문은 이를 해결하기위해 Deep Planning Network(PlaNet)을 제시합니다.

Introduction

• Planning을 위해 해결해야 하는 문제에는 model의 정확도로 인한 error가 누적되는 문제, 다양한 미래의 결과에 대한 정보를 모두 담지 못하는 문제, unseen혹은 잘 학습되어지지 않은 state에 대한 uncertainty를 가지지 않는다는 문제들이 있습니다. 이런 문제에도 model을 사용한 planning의 장점으로는 data efficiency 증가, 성능 증가, 학습한 dynamics에 대한 다양한 task에 transfer할 수 있다는 장점이 있습니다.

• 본 논문의 contribution은 다음과 같습니다.

  • Planning in latent spaces

    • image based task에서 latent space만을 가지고 planning을 진행합니다.

  • Recurrent state space model

    • Model은 environment의 deterministic과 stochastic함을 모두 잡을 수 있도록 설계되었습니다.

  • Latent overshooting

    • Model은 multi step에 대한 prediction을 통해 environment를 배웁니다.

Latent Space Planning

• Model을 학습시키기 위해서 unknown environment로 부터 data를 모으고, 모은 data를 가지고 dynamic model을 학습시키는 행위를 반복해야 합니다. 이번 섹션에서는 notation과 전체적인 algorithm에 대해 설명합니다.

• Problem Setup

  • environment에 대해 agent는 partially observable Markov decision process(POMDP)를 가정하여 학습합니다. 이 때 discrete time step \(t\), hidden states \(s_t\), image observation \(o_t\), continuous action vectors \(a_t\), scalar rewards \(r_t\)와 다음의 dynamics를 정의합니다.

  • Transition function : \(s_t \sim \textnormal{p}(s_t \vert s_{t-1},a_{t-1})\)

  • Observation function : \(o_t \sim \textnormal{p}(o_t \vert s_t) \ \ (s_0 : \mathrm{fixed\ init\ state})\)

  • Reward function : \(r_t \sim \textnormal{p}(r_t \vert s_t)\)

  • Policy : \(a_t \sim \textnormal{p}(a_t \vert o_{\leq t},a_{<t})\)

  • Goal : \(E_\textnormal{p}[\sum^T_{t=1}r_t]\)

  • function은 \(\textnormal{p}\)로 표현하고, model은 \(p\)로 표현합니다.

• Model-based planning

  • PlaNet은 transition model과 observation model과 reward model 뿐만아니라 encoder \(q(s_t \vert o_{\leq t}, a_{<t})\)를 가지는데, 이는 filtering이란 표현과 함께 production으로 나타내는데 section 3에서 다시 수식에 대해 설명하도록 하겠습니다.

  • Model Predictive control의 형태로 학습이 진행되는데, 각 step마다 planning을 하고 action을 실행한 뒤 replanning을 하는 형태로 이루어 집니다. 즉, 기존 RL처럼 policy나 value network를 사용하지 않는 hybrid형태의 학습 방법 입니다.

• Experience collection

  • random action을 통해 얻은 data \(S\)를 통해 model을 학습하기 시작합니다. 이후 data추가는 각 \(C\) step마다 이루어지게 됩니다. 또한, planner를 통해 얻은 action에는 Gaussian noise를 추가해줍니다. 마지막으로, environment에 유의미한 변화를 만들기 위해 action을 \(R\)번 반복합니다.

• Planning algorithm

  • Planning을 위한 algorithm에는 Cross entropy method를 사용합니다. 이를 나타내면 다음과 같습니다.

    

    각 action은 time혹은 state에 dependent한 H길이의 planning을 하게 됩니다. 이 때 \(J\)개의 후보를 뽑아 planner를 optimization하고, 이를 \(I\)번 진행 후 \(\mu_t\)를 통해 action을 결정하게 되고, 이후 step에 대해 다시 초기화 시켜 local optimum에 빠지는 것을 방지합니다. 이 때, 모든 연산은 environment가 개입되어 있지 않은 latent state상에서 이루어지므로 병렬적으로 이루어질 수 있고, 이러한 population-based optimizer를 사용했을 때 많은 양의 다른 sequences를 비교하면 한 trajectory내에서 다양한 action을 비교하지 않아도 충분하다고 합니다.

Recurrent State Space Model

• latent space를 표현하기 위해 본 논문에서는 Recurrent state-space model(RSSM)을 사용합니다.

• Latent Dynamics

  • 학습을 위해 data sequences \(\{o_t,a_t,r_t\}^T_{t=1}\)를 정의합니다. 그리고 모델을 정의하면 다음과 같습니다.

    • Transition model : \(s_t \sim p(s_t \vert s_{t-1},a_{t-1})\)

      • Transition model은 feed forward neural network로, Gaussian mean과 variance를 output으로 가집니다.

    • Observation model : \(o_t \sim p(o_t \vert s_t)\)

      • Observation model은 deconvolutional neural network로 Gaussian mean과 identity covariance를 가집니다.

    • Reward model : \(r_t \sim p(r_t \vert s_t)\)

      • Reward model은 feed-forward neural network로 Gaussian mean과 unit variance를 가집니다.

• Variational Encoder

  • encoder는 이전 연구들과 다르게 다음과 같이 state posterior를 오직 바로 이전의 observation과 action의 product꼴로 가정합니다. 이를 filtering이라고 칭합니다.

    \[q(s_{1:T} \vert o_{1:T},a_{1:T}) = \prod^T_{t=1} q(s_t \vert s_{t-1}, a_{t-1},o_t)\]

    이는 observation을 받는 convolutional neural network와 state로 변환하는 feed forward neural network로 이루어져 있습니다.

• Training Objective

  • model을 학습시키기 위해서 다음과 같은 prior를 정의합니다.(reward는 생략하지만 observation과 같이 joint probability로 등장해야함이 자명합니다.)

    \[\ln p(o_{1:T} \vert a_{1:T}) \triangleq \ln \mathbb{E}_{p(s_{1:T \vert a_{1:T}})}[\prod^T_{t=1} p(o_t\vert s_t)]\]

    left term의 prior은 right term과 같이 latent state에 대한 observation의 posterior로 정의할 수 있습니다. 그리고, elbo를 사용해 이 posterior를 optimize하자면 다음과 같습니다.

    \[=\ln \mathbb{E}_{q(s_{1:T} \vert o_{1:T},a_{1:T})}[\prod^T_{t=1}p(o_t \vert s_t) p(s_t \vert s_{t-1},a_{t-1})/ q(s_t \vert o_{\leq t},a_{<t})]\]

    Jensen’s Inequality에 의해

    \[\geq\ln \mathbb{E}_{q(s_{1:T} \vert o_{1:T},a_{1:T})}[\sum^T_{t=1}\ln p(o_t \vert s_t)+\ln p(s_t \vert s_{t-1},a_{t-1})-\ln q(s_t \vert o_{\leq t},a_{<t})]\] \[= \sum^T_{t=1} (\mathbb{E}_{q(s_t\vert o_{\leq t},a{<t})}[\ln p(o_t \vert s_t)] - \mathbb{E}_{q(s_{t-1}\vert o_{\leq{t-1}},a_{<a-1})}[\mathrm{KL}[q(s_t \vert o_{\leq t},a_{<t}\Vert p(s_t \vert s_{t-1},a_{t-1})]]\]

    다음과 같은 maximization해야하는 objective를 얻을 수 있습니다.

• Deterministic path

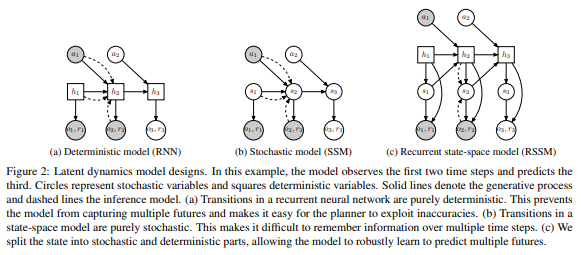
  • Transition model을 stochastic하게 만드는 것도, deterministic하게 만드는 것도 각각 문제가 존재합니다. 그렇기에 transition model을 두 가지 속성을 모두 결합해 이 문제들을 해결 하였는데, 이는 다음과 같습니다.

    

    그림(c)와 같은 방식이 RSSM이고, recurrent neural network를 도입해 environment를 deterministic한 hidden(belief)으로 표현하고 여기서 mean과 standard deviation을 output으로 가져 stochastic state를 표현할 수 있게 됩니다.

Latent Overshooting

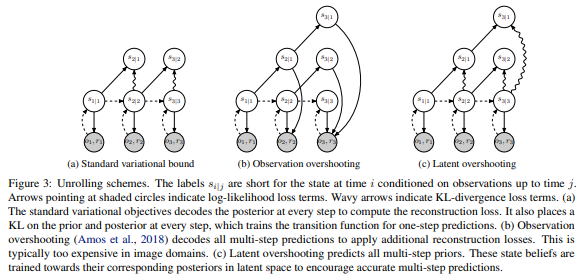
• 기존의 방법으로 model을 학습하는데 있어 \(p(s_t \vert s_{t-1},a_{t-1})\)는 오직 한 step에 대해서만(\(p(s_t \vert o_t)\)와 KL divergence를 계산하였으나, 다음 그림과 같이 multi step에 대한 latent와 KL divergence를 계산하여 update하는 latent overshooting을 사용합니다.

  

  이를 통해 그림 (c)와 같이 \(s_{3\vert 1}\)은 \(s_{3\vert 3}\)에 의해 학습될 수 있습니다. 이 경우 \(s_{3\vert 3}\)의 gradient는 고정된 상태입니다. 이는 다른 algorithm과 결합되었을 때 성능향상에 꽤 도움이 되었지만, RSSM에는 크게 좋은 영향을 끼치진 못했습니다.

  

• Limited Capacity

  • 만약 model이 정말 완벽한 one-step prediction이 가능하다면 완벽한 multi-step prediction도 가능하겠지만 model 표현의 capacity와 distribution을 특정 분포로 가정했기 때문에 이는 불가능에 가깝습니다. 그렇기 위해 이어서 설명하고 있는 multi step distance에 대해 다 더해주는 형식으로 model을 학습합니다.

• Multi-step Prediction

  • 위에서 정의했던 one step posterior을 좀더 generalization합니다. 이는 생략하도록 합니다. 멀리 있는 state와 mutual information이 좀 더 작을 것이라는 추측을 통한 bound도 제시하는데 흥미로웠습니다.

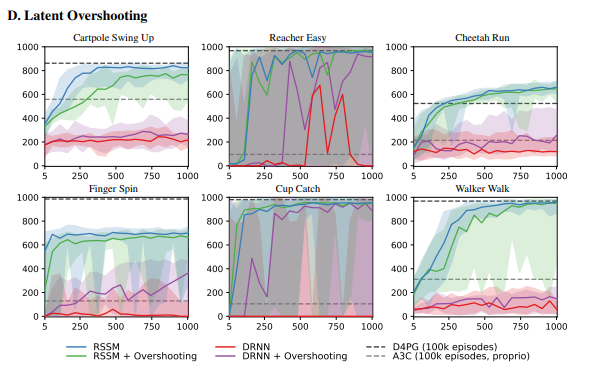
• Latent Overshooting

  • 모든 distance에 대해 KL divergence를 구해주는 식으로 model을 학습시키는 형태도 제시합니다.

    \[\frac{1}{D}\sum^D_{d=1} \ln p_d(o_{1:T}) \geq \sum^T_{t=1}(E_{q(s_t \vert o\leq t)}[\ln p(o_t \vert s_t)] - \frac{1}{D}\sum^D_{d=1}\beta_d \mathbb{E}_{p(s_{t-1}\vert s_{t-d})q(s_{t- d} \vert o\leq {t-d})}\mathrm{KL}[q(s_t\vert o_{\leq t}) \Vert p(s_t \vert s_{t-1}) ])\]

References

• Learning Latent Dynamics for Planning from Pixels