Self-Supervised Policy Adaptation During Deployment
Abstract
- 한 environment에서 학습시킨 agent를 다른 environment에서 deploy해야하는 상황들이 많이 있습니다. 이를 위해 policy를 다른 많은 environment들을 대비하여 generalization하는 일은 사실 굉장히 어렵습니다. 그렇기에 policy를 새로운 environment에서 reward signal없이 학습시키는 것(adaption)이 자연스러운 해답으로 등장하였고, 본 논문은 이를 구체적으로 제시합니다.
Introduction
-
abstract에서 언급한 것 처럼, robust policy를 만드는 것이 기존에 많이 연구되었습니다. 그렇기에 주로 augmented environment를 통해 policy를 학습하였고, 이 augmented environment가 실제 test environment를 cover할 수 있기를 바라야했습니다. 그러나 test environment에 대한 정보가 전혀 알려지지 않은 상황을 가정해야하므로 이를 학습시키는 일은 input dimension이 커질수록 더많은 sample을 학습시켜야하고, 또한 이런 augmented environment가 test environment와 오히려 너무 연관성이 없을 때 성능에 악영향을 끼치기도 합니다. 그렇기에 인간이 test environment를 예측하고 이에 대한 대비로 augmented environment를 만들어야 하므로 비효율적입니다.
-
반면에 policy adaption은 위의 robust policy의 단점을 해결할 수 있습니다. 이는 가장 간단하게 policy를 fine-tune하는 방법으로 생각을 해 볼 수 있는데, 기존 연구들은 학습 중 dense reward function을 이용할 수 있었고, deploy중 추가적인 engineering이 필요했습니다. 본 논문은 self-supervised learning방법을 통해 이러한 문제들을 해결합니다.
-
학습 방법은 다음과 같습니다. 기본적인 RL objective와 함께, observation의 representation을 배울 수 있는 추가적인 objective를 추가하여 training단계에서 둘을 같이 사용해 학습하며, test(deploy)때 후자의 objective만 이용해 새로운 environment에 adapt하는 방법을 사용합니다.
Related Work
-
Self-supervised Learning
- labeling없이 visual representation을 배울 수 있는 효과적인 방법으로, auxiliary objective를 만들거나 data augmentation을 통한 방법이 주로 이루어졌습니다.
-
Generalization Across Different Distributions
- domain adaption분야에선 다양한 연구들이 이루어졌지만, 본 연구는 truly unseen, adaptive policy에 대한 방법을 제시합니다.
-
Test-time Adaptation for Deep Learning
- 주로 computer vision계열에서 test-time때 adaption하는 연구들이 이루어졌지만, 본 논문은 이를 RL적으로 접근하였습니다.
Method
-
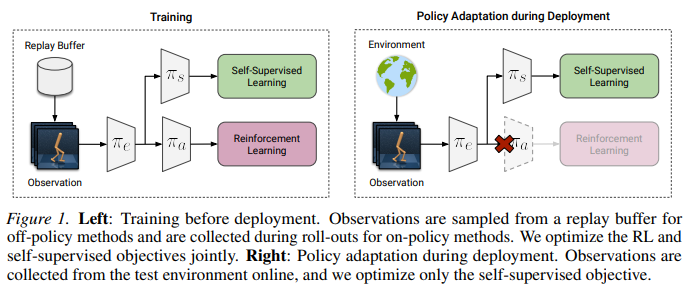
본 논문은 이 알고리즘을 Policy Adaptation during Deployment(PAD)라는 이름으로 제시합니다.이는 on-policy, off-policy 모두 적용 가능합니다. 먼저 architecture에 대한 그림을 올려놓고 아래서 설명하도록 하겠습니다.
-
Network Architecture
- network parameter \(\theta\)에 대해 feature extractor의 parameter \(\theta_e\), feature extractor 이 후 action에 대한 distribution을 생성하는 parameter \(\theta_a\), feature extractor 이후 self-supervised-learning을 하도록 붙은 parameter \(\theta_s\) 로 나타낼 수 있습니다. 그리고 어떤 parameter 가진 network를 다음과 같이 표현합니다. feature extractor의 parameter \(\theta_e\)를 가진 network \(\pi_e\)는 다음과 같이 표기합니다. 이를 통해 image observation \(\boldsymbol{s}\)에 대해 \(\pi(\boldsymbol{s};\theta) = \pi_a(\pi_e(\boldsymbol{s})),\ (\theta = (\theta_e,\theta_a))\)다음과 같이 나타낼 수 있습니다.
-
Inverse Dynamics Prediction And Rotation Prediction
-
self-supervised learning을 위해서 다양한 방식을 생각해 볼 수 있습니다. observed state에 대해 rotation 하여 이를 맞추는 prediction문제로 이 \(\pi_s\)를 학습할 수도 있지만, inverse dynamics prediction에 대해 좀 더 초점을 맞춰서 보겠습니다.
-
각 step마다 얻게되는 transition sequence는 다음과 같습니다.
\[(\boldsymbol{s}_t,\boldsymbol{a}_t,\boldsymbol{s}_{t+1})\]이 때, state와 next state를 input으로 받아, action을 prediction하는 문제로 self-supervised learning문제를 formulation합니다. loss는 다음과 같이 나타낼 수 있습니다.
\[L(\theta_s,\theta_e) = \ell(\boldsymbol{a}_t, \pi_s(\pi_e(\boldsymbol{s}_t),\pi_e(\boldsymbol{s}_{t-1})))\]\(\ell\)은 continuous action space일 때, 실제 action과 prediction의 mean squared error loss, discrete action일 때, cross-entropy loss 입니다. 이 때, continuous action space에서 이 self-supervised learning이 좀 더 효과적인데 이는 작은 discrete action space일 때 이를 통해 얻는 유의미한 정보가 좀 더 적기 때문입니다. 또한 forward dynamics를 하지 않는 이유도 state action을 통해 next state를 예측하는 일은 feature space가 유의미하지 않을 확률이 있기 때문입니다.
-
-
Training and Testing
-
policy가 deploy되기 전에 agent는 기존 environment의 reward와 함께 auxiliary task에 대한 loss를 통해 학습이 진행됩니다. 이는 목적함수를 최소화 시키는 기존 RL의 objective와 함께 다음과 같이 표현할 수 있습니다.
\[\min_{\theta_a,\theta_s,\theta_e}J(\theta_a,\theta_e)+\alpha L(\theta_s,\theta_e),\ \ \alpha > 0\]이 때, deploy하게 되면, reward가 없는 상태이므로, \(\theta_a\)를 학습하지 않게 됩니다. 오직 \(L(\theta_s,\theta_e)\)를 통해 이를 업데이트 하게 되는데, \(\theta_s\)를 fix시키는 것과 fix하지 않는 것 둘의 차이는 실험적으로 아주 적었습니다. 그리하여 deploy때 update되는 \(\theta_s, \theta_e\)는 다음과 같습니다.
\[\boldsymbol{s}_t \sim p(\boldsymbol{s}_t \vert \boldsymbol{a}_{t-1},\boldsymbol{s}_{t-1})\] \[\theta_s(t) = \theta_s(t-1)-\nabla_{\theta_s}L(\boldsymbol{s}_t;\theta_s(t-1),\theta_e(t-1))\] \[\theta_e(t) = \theta_e(t-1)-\nabla_{\theta_e}L(\boldsymbol{s}_t;\theta_s(t-1),\theta_e(t-1))\] \[\boldsymbol{a}_t =\pi(\boldsymbol{s}_t ; \theta(t)),\ \theta(t) = (\theta_e(t),\theta_a)\]\(p\)는 deploy때의 unknown environment transition에 대한 probability, \(L\)은 self-supervised objective, \(\boldsymbol{s}_0\)는 environment에 의해 정해지는 initial state, \(\boldsymbol{a}_0=\pi_\theta(\boldsymbol{s}_0)\), \(\theta_s(0)=\theta_s,\theta_e(0)=\theta_e\)입니다.
-