Mastering Atari With Discrete World Models 논문 리뷰 및 설명

Mastering Atari With Discrete World Models

Abstract

• World model은 agent가 imaged outcome으로부터 학습할 수 있도록 합니다. 이러한 world model을 이용한 model-based algorithm은 최근 몇몇 task에서 굉장한 성능을 보였으나 아직도 정확한 world model을 만드는 것에 대해서는 해결하지 못한 문제 중 하나입니다. 논문은 Dreamer를 기반으로한 Dreamer-V2를 설명하는데 이는 기존 Dreamer와 다르게 compact discrete latent를 사용하고, KL loss를 balancing하는 테크닉을 이용합니다. 이로 인해 처음으로 world-model을 가지고 Atari에서 인간 수준의 performance를 뛰어넘는 성능을 보입니다.

Introduction

• World model을 사용하는 것은 environment에 대해 agent의 knowledge를 나타내는 방법 중 하나 입니다. model-free method와는 다르게 world model은 agent가 planning을 할 수 있도록 environment를 generalization합니다.

• 이런 world model은 다양한 방법으로 응용이 가능하게 되고, Input이 high-dimensional image일 때, compact state로 encoding하여 model을 사용하면 cumulative error가 줄어들고 병렬화에 장점이 생깁니다. 이를 이용해 Dreamer가 다양한 continuous control task에서 좋은 성능을 보였습니다.

• 이럼에도 불구하고 world model의 정교함은 아직도 연구가 필요한데, 본 논문은 이를 Dreamer-V2를 통해 개선함을 보입니다.

DreamerV2

World Model Learning

• Experience Dataset
  • agent의 dataset은 images, actions, rewards, discount factors \(x_{1:t},a_{1:t},r_{1:t},\gamma_{1:t}\)로 구성되며, \(\gamma\)는 0.999로 고정되었다가 마지막 time step에서 0이 됩니다. batch size는 50, trajectory length도 50으로 random sampling하여 학습하게 됩니다.
• Model Components

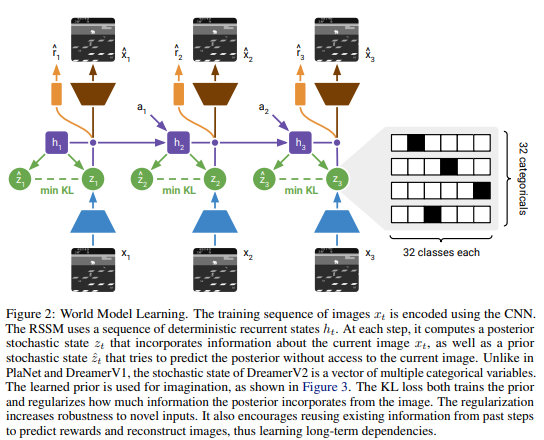
  • Recurrent State-Space Model(RSSM)은 아래 그림과 같이 deterministic recurrent states(belief) \(h_t\)를 만들고, 이를 이용해 stochastic하게 \(z\)와 \(\hat{z}\)를 만듭니다.

    

    \(z, \hat{z}\)이 둘은 각각 belief(variational parameter정도의 해석)에 의해 생성된 posterior와 prior정도로 생각할 수 있고 본문에서도 그렇게 표현하였습니다. 각 components를 수식으로 나타내면 다음과 같습니다.

    \[\mathrm{Recurrent\ model} : h_t= f_\phi(h_{t-1},z_{t-1},a_{t-1})\] \[\mathrm{Representation\ model} : z_t \sim q_\phi(z_t \vert h_t,x_t)\] \[\mathrm{Transition\ predictor} : \hat{z}_t \sim p_\phi(\hat{z}_t \vert h_t)\] \[\mathrm{Image\ predictor} : \hat{x}_t \sim p_\phi(\hat{x}_t \vert h_t,z_t)\] \[\mathrm{Reward\ predictor} : \hat{r}_t \sim p_\phi(\hat{r}_t \vert h_t,z_t)\] \[\mathrm{Discount\ predictor} : \hat{\gamma}_t \sim p_\phi(\hat{\gamma}_t \vert h_t,z_t)\]

    Discount factor는 이전 논문들에선 주로 언급만되었지만 여기서는 주요 component로 사용합니다.

• Neural Networks
• Distributions
  • Image predictor는 transposed CNN을 통해 diagonal Gaussian의 likelihood mean을 output으로 가집니다.
    • Reward predictor는 univariate Gaussian의 likelihood mean을 가집니다.
    • Discount Bernoulli likelihood를 가집니다.

    • 기존엔 Latent에 대해 diagonal Gaussian을 가지고, reprameterization trick을 통해 update했지만, Dreamer-V2는 categorical variable을 가지고 straight-through gradient를 통해 update합니다. 이는 다음과 같습니다.

      

• Loss function

  • 각 component는 결합되어(chain rule로인해) 학습됩니다. transition predictor에 의해 생성된 \(\hat{z}\)를 가지고 image predictor, reward predictor, discount predictor는 분포를 생성하며 이들은 log-likelihood를 maximize하도록 학습됩니다. representation model은 이러한 \(\hat{z}\)를 정교하게 만들기 위한 학습을 합니다. 그리고 entropy를 통해 distribution을 regularize할수도 있습니다. 이를 표현한 식은 다음과 같습니다.

    \[\mathcal{L}(\phi)=\mathbb{E}_{q_\phi(z_{1:T}\vert a_{1:T},x_{1:T})} = [\sum^T_{t=1}-\ln p_\phi(x_t\vert h_t,z_t)-\ln p_\phi(r_t\vert h_t,z_t)-\ln p_\phi(\gamma_t\vert h_t,z_t)+\beta\mathrm{KL}[q_\phi(z_t\vert h_t,x_t) \Vert p_\phi(z_t\vert h_t)]] \cdots(2)\]

    benchmark마다(continuous vs discrete) \(\beta\)를 조절해주는 것이 좋은 효과를 냈습니다.

• KL balancing

  • (2)에서의 식을 통해 world model의 loss는 ELBO나 action sequence에 의해 condition된 hidden Markov model의 variational free energy와 같은 형식임을 보았습니다. 이를 통해 sequential VAE처럼 해석할 수 있는데 ELBO objective에서의 KL loss는 다음과 같은 두가지 역할을 하게 됩니다. prior \(\hat{z}\)를 representation \(z\)와 같도록 학습시키는 것, representation \(z\)를 regularized하는 것 입니다. 하지만 잘학습되지 않은 prior가지고 regularize하는 것은 학습에 방해가 되므로 아래와 같이 weight을 다르게 주어 학습함을 보입니다. 이를 KL balancing이라고 합니다.

    

Behavior Learning

• 기본적으로 actor와 critic이 update될때 model은 fix되어 update되지 않음을 기본으로 합니다.
• Imagination MDP
  • Initial states \(\hat{z}_0\)는 world model training중의 distribution을 따릅니다. 이로부터 transition predictor \(p_\phi(\hat{z}_t \vert \hat{z}_{t-1},\hat{a}_{t-1})\)를 통해 compact state \(\hat{z}_{1:H}\)를 얻을 수 있고 마찬가지로 reward predictor와 discount predictor로 인해 agent는 MDP상황에서 학습할 수 있게 됩니다.
• Model Components

  • stochastic actor, deterministic critic을 사용합니다.

    \[\mathrm{Actor} : \hat{a} \sim p_\psi(\hat{a}_t \vert \hat{z}_t)\] \[\mathrm{Critic} : v_\xi(\hat{z}_t) \approx \mathbb{E}_{p_\phi,p_\psi}[\sum_{\tau \geq t} \hat{\gamma}^{\tau-t}\hat{r}_\tau]\]
• Critic Loss Function

  • n-step learning을 위해 target을 다음과 같이 recursive하게 구합니다.

    \[V^\lambda_t = \hat{r}_t+\hat{\gamma}_t\left\{\begin{matrix}(1-\lambda) v_\xi (\hat{z}_{t+1})+\lambda V^\lambda_{t+1}\ \mathrm{if}\ t < H\\ v_\xi(\hat{z}_H)\ \mathrm{if} \ t=H\end{matrix}\right.\]

    이렇게 얻은 target을 가지고 critic loss는 다음과 같이 구합니다. \(\mathrm{sg}\)는 stop gradient를 의미합니다.

    \[\mathcal{L}(\xi) = \mathbb{E}_{p_\phi,p_\psi}[\sum^{H-1}_{t=1}\frac{1}{2}(v_\xi(\hat{z}_t)-\mathrm{sg}(V^\lambda_t))^2]\]
• Actor loss function

  • actor는 predicted long term future reward를 maximize하도록 update합니다. 여기서 high-variance and unbiased term과 low-variance biased term을 mixing하여 benchmark마다 다르게 사용했습니다. 전자는 REINFORCE algorithm으로 unbiased gradient를 얻지만 초반 학습이 느립니다. 후자는 논문에서 dynamics backprop으로 표현했는데, compact state에서 agent가 행한 action에 대해 straight-through gradients를 통해 update하겠다는 의미입니다. entropy term을 추가한 식을 나타내면 다음과 같습니다.

    \[\mathcal{L}(\psi) = \mathbb{E}_{p_\phi,p_\psi}[\sum^{H-1}_{t=1}(- \rho \ln p_\psi(\hat{a}_t \vert \hat{z}_t)\mathrm{sg}(V^\lambda_t-v_\xi(\hat{z}_t)) - (1-\rho)V^\lambda_t - \eta H[a_t\vert\hat{z}_t])]\]

Experiments

• 생략합니다.

References

• Mastering Atari with Discrete World Models